LOJ#2541 猎人杀

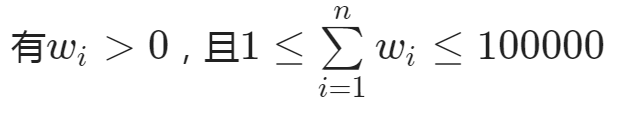
解：step1：猎人死了之后不下台，而是继续开枪，这样分母不变......

然后容斥，枚举猎人集合s，钦定他们在1之后死。定义打到1的时候结束，枚举游戏在i轮时结束。

发现式子是一个1 + x + x² + x³ + ... = 1 / (1 - x)

但是枚举子集不现实，发现值域很小，我们用小Z的礼物的套路，考虑计算每个值的容斥系数是多少。

然后就NTT加速了。预处理逆元卡常。

 #include <bits/stdc++.h>

 typedef long long LL;
 typedef std::vector<int> Poly;

 inline void read(int &x) {
     x = ;
     char c = getchar();
     while(c < '' || c > '') c = getchar();
     while(c >= '' && c <= '') {
         x = x *  + c - ;
         c = getchar();
     }
     return;
 }

 const int N = , MO = ;

 int A[N << ], B[N << ];
 int r[N << ], n, w[N], inv[N];

 inline int qpow(int a, int b) {
     a = (a % MO + MO) % MO;
     int ans = ;
     while(b) {
         if(b & ) ans = 1ll * ans * a % MO;
         a = 1ll * a * a % MO;
         b = b >> ;
     }
     return ans;
 }

 inline void prework(int n) {
     static int R = ;
     if(R == n) return;
     R = n;
     int lm = ;
     while(( << lm) < n) lm++;
     for(register int i = ; i < n; i++) r[i] = (r[i >> ] >> ) | ((i & ) << (lm - ));
     return;
 }

 inline void NTT(int *a, int n, int f) {
     prework(n);
     for(int i = ; i < n; i++) {
         if(i < r[i]) std::swap(a[i], a[r[i]]);
     }
     for(register int len = ; len < n; len <<= ) {
         int Wn = qpow(, (MO - ) / (len << ));
         if(f == -) Wn = qpow(Wn, MO - );
         for(register int i = ; i < n; i += (len << )) {
             int w = ;
             for(register int j = ; j < len; j++) {
                 int t = 1ll * a[i + len + j] * w % MO;
                 a[i + len + j] = (a[i + j] - t) % MO;
                 a[i + j] = (a[i + j] + t) % MO;
                 w = 1ll * w * Wn % MO;
             }
         }
     }
     if(f == -) {
         LL inv = qpow(n, MO - );
         for(int i = ; i < n; i++) {
             a[i] = 1ll * a[i] * inv % MO;
         }
     }
     return;
 }

 inline Poly mul(const Poly &a, const Poly &b) {
     int na = a.size(), nb = b.size(), n = na + nb - , len = ;
     while(len < n) len <<= ;
     for(register int i = ; i < na; i++) A[i] = a[i];
     for(register int i = ; i < nb; i++) B[i] = b[i];
     memset(A + na, , (len - na) * sizeof(LL));
     memset(B + nb, , (len - nb) * sizeof(LL));
     NTT(A, len, ); NTT(B, len, );
     for(register int i = ; i < len; i++) A[i] = 1ll * A[i] * B[i] % MO;
     NTT(A, len, -);
     Poly ans(n);
     for(register int i = ; i < n; i++) ans[i] = A[i];
     return ans;
 }

 Poly solve(int l, int r) {
     if(l == r) {
         Poly a(w[r] + );
         a[] = ; a[w[r]] = -;
         return a;
     }
     int mid = (l + r) >> ;
     return mul(solve(l, mid), solve(mid + , r));
 }

 int main() {
     int sum = ;
     read(n);
     for(register int i = ; i <= n; i++) {
         read(w[i]);
         sum += w[i];
     }

     inv[] = inv[] = ;
     for(int i = ; i <= sum; i++) {
         inv[i] = 1ll * inv[MO % i] * (MO - MO / i) % MO;
     }

     std::sort(w + , w + n + );
     Poly a = solve(, n);

     int m = a.size();
     int ans = ;
     for(register int i = ; i < m; i++) {
         ans = (ans + 1ll * a[i] * inv[w[] + i] % MO) % MO;
     }
     ans = 1ll * ans * w[] % MO;
     printf("%d\n", (ans + MO) % MO);
     return ;
 }

AC代码