LG1955 [NOI2015]程序自动分析

题意

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设x1,x2,x3...代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2,x2=x3,x3=x4,x4≠x1，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入输出格式

输入格式：

从文件prog.in中读入数据。

输入文件的第1行包含1个正整数t，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第1行包含1个正整数n，表示该问题中需要被满足的约束条件个数。接下来n行，每行包括3个整数i,j,e，描述1个相等/不等的约束条件，相邻整数之间用单个空格隔开。若e=1，则该约束条件为xi=xj；若�e=0，则该约束条件为xi≠xj；

输出格式：

输出到文件 prog.out 中。

输出文件包括t行。

输出文件的第 k行输出一个字符串“ YES” 或者“ NO”（不包含引号，字母全部大写），“ YES” 表示输入中的第k个问题判定为可以被满足，“ NO” 表示不可被满足。

输入输出样例

输入样例#1：
复制

2
2
1 2 1
1 2 0
2
1 2 1
2 1 1

输出样例#1：
复制

NO
YES

输入样例#2：
复制

2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0

输出样例#2：
复制

YES
NO

说明

【样例解释1】

在第一个问题中，约束条件为：x1=x2,x1≠x2。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：x1=x2,x1=x2。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4，然而最后一个约束条件却要求x1≠x4，因此不可被满足。

【数据范围】

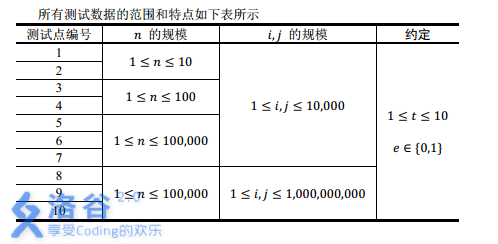
【时限2s，内存512M】

分析

离散化后，先处理相等的，用并查集。再看看不等的是否位于同一并查集中即可。

时间复杂度\(O(n \log n)\)

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;
co int N=1e5+1;
int n,m,a[N*2],fa[N*2];
struct P{
	int i,j;
	bool e;
}p[N];
int get(int x) {return fa[x]==x?x:fa[x]=get(fa[x]);}
int find(int x) {return lower_bound(a+1,a+m+1,x)-a;}
void cxzdfx(){
	read(n);
	for(int i=1;i<=n;++i){
		read(p[i].i),read(p[i].j),read(p[i].e);
		a[2*i-1]=p[i].i,a[2*i]=p[i].j;
	}
	sort(a+1,a+2*n+1),m=unique(a+1,a+2*n+1)-(a+1);
	for(int i=1;i<=m;++i) fa[i]=i;
	for(int i=1;i<=n;++i)
		if(p[i].e) fa[get(find(p[i].i))]=get(find(p[i].j));
	for(int i=1;i<=n;++i)
		if(!p[i].e&&get(find(p[i].i))==get(find(p[i].j)))
			return puts("NO"),void();
	puts("YES");
}
int main(){
//	freopen(".in","r",stdin),freopen(".out","w",stdout);
	int kase=read<int>();
	while(kase--) cxzdfx();
	return 0;
}