FM与FFM深入解析

因子机的定义

机器学习中的建模问题可以归纳为从数据中学习一个函数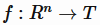，它将实值的特征向量映射到一个特定的集合中。例如，对于回归问题，集合 T 就是实数集 R，对于二分类问题，这个集合可以是{+1，-1}。对于监督学习，通常有一标注的训练样本集合

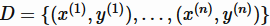
线性函数是最简单的建模函数，它假定这个函数可以用参数w来刻画，

对于回归问题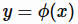，，而对于二分类问题，需要做对数几率函数变换（逻辑回归）

线性模型的缺点是无法学到模型之间的交互，而这在推荐和CTR预估中是比较关键的。例如，CTR预估中常将用户id和广告id onehot 编码后作为特征向量的一部分。

为了学习特征间的交叉，SVM通过多项式核函数来实现特征的交叉，实际上和多项式模型是一样的，这里以二阶多项式模型为例

多项式模型的问题在于二阶项的参数过多，设特征维数为n，那么二阶项的参数数目为n(n-1)/2,对于广告点击率预估问题，由于存在大量id特征，导致n可能为10⁷维，这样一来，模型参数的量级为10¹⁴，这比样本量4x10⁷多得多！这导致只有极少数的二阶组合模式才能在样本中找到，而绝大多数模式在样本中找不到，因而模型无法学出对应的权重。例如，对于某个w_ij样本中找不到x_i=1，x_j=1（这里假定所有的特征都是离散的特征，只取0和1两个值）这种样本，那么w_ij的梯度恒为0，从而导致参数学习失败！

很容易想到，可以对二阶项参数施加某种限制，减少模型参数的自由度。FM 施加的限制是要求二阶项系数矩阵是低秩的，能够分解为低秩矩阵的乘积

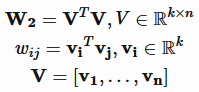
这样一来，就将参数个数减少到kn，可以设置较少的k值（一般设置在100以内，k<<n)，极大地减少模型参数，增强模型泛化能力，这跟矩阵分解的方法是一样的。向量v_i可以解释为第i个特征对应的隐因子或隐向量。以user和item的推荐问题为例，如果该特征是user，可以解释为用户向量，如果是item，可以解释为物品向量。

计算复杂度

因为引入和二阶项，如果直接计算，时间复杂度将是O(n²),n是特征非零特征数目，可以通过简单的数学技巧将时间复杂度减少到线性时间复杂度。

基于一个基本的观察，齐二次交叉项之和可以表达为平方和之差

上式左边计算复杂度为O(n²)，而右边是O(n),根据上式，可以将原表达式中二次项化简为

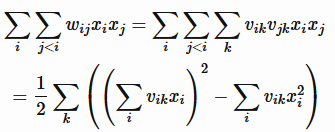
上式计算时间复杂度是O(n)

基于梯度的优化都需要计算目标函数对参数的梯度，对FM而言，目标函数对参数的梯度可以利用链式求导法则分解为目标函数对Φ的梯度和∂Φ/∂θ的乘积。前者依赖于具体任务，后者可以简单的求得

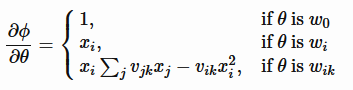
优化方案

原论文中给出了三种优化方案，它们分别是

随机梯度下降，这种方案收敛慢而且非常敏感，可以利用现代的一些trick，例如采用 AdaGrad 算法，采用自适应学习率，效果相对比较好，论文[6]对FFM就采用这种方案。
交替方向乘子(ALS)，这种方案只适用于回归问题，它每次优化一个参数，把其他参数固定，好处是每次都是一个最小二乘问题，有解析解。
基于蒙特卡罗马尔科夫链的优化方案，论文中效果最好的方案，细节可以参考原文。

FFM

在实际预测任务中，特征往往包含多种id，如果不同id组合时采用不同的隐向量，那么这就是 FFM(Field Factorization Machine) 模型[6]。它将特征按照事先的规则分为多个场(Field)，特征x_i属于某个特定的场f，每个特征将被映射为多个隐向量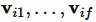，每个隐向量对应一个场。当两个特征x_i，x_j组合时，用对方对应的场对应的隐向量做内积！

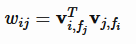
f_i，f_j分别是特征x_i，x_j对应的场编号。FFM 由于引入了场，使得每两组特征交叉的隐向量都是独立的，可以取得更好的组合效果，但是使得计算复杂度无法通过优化变成线性时间复杂度，每个样本预测的时间复杂度为O(n² k)，不过FFM的k值通常远小于FM的k值。有论文对FFM在Criteo和Avazu两个任务（Kaggle上的两个CTR预估比赛）上进行了试验，结果表明 FFM 的成绩优于 FM。事实上，FM 可以看做只有一个场的 FFM。