OpenGL光照计算中法线矩阵原理及推到过程

问题起源

在计算漫反射关照时,需要用到法线,通过法线和光线的点乘值,计算漫反射的产生的光线强度,所以需要从顶点着色器中将法线数据传递到片源着色器中,但是片源着色器中的顶点坐标是经过了模型矩阵变化过的世界坐标.所以二者很可能已经不匹配了,当然模型矩阵是单位矩阵的特殊情况下,就没有影响.

对法线进行mv变换

因此,需要对法线也应用mv矩阵变换.这样,模型的在旋转和缩放后,法线才能也与之匹配,如下图这样:

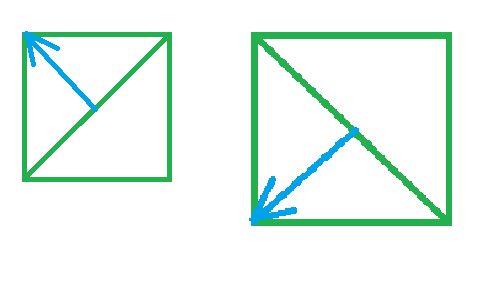
去掉对法线的偏移效果

但有个问题,就是偏移,如果法线跟着一起偏移,方向就会出问题了,加入模型矩阵沿x方向偏移一点,法线的x也相应的增加一点,就会出现下面这样的情况:



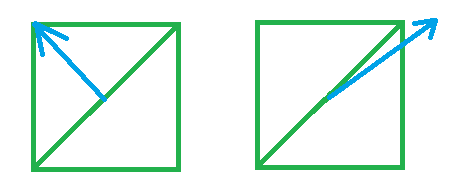
这种情况可以通过将法线的齐次坐标设置为0,来解决,因为偏移的原理就是矩阵最后一列的值乘以其次坐标产生的影响:

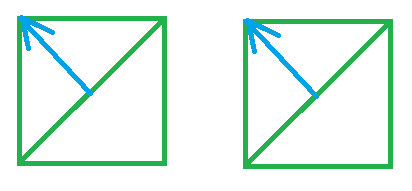
不等比缩放

大部分情况下,上面的处理就可以得到想要的效果了,但是,如果mv矩阵中存在不等比缩放,那么会出现法线与原来的面不垂直的问题,虽然在很多情况下这个效果可能不会太明显,因为法线偏差一点点,关照计算并不会有特别明显的区别:



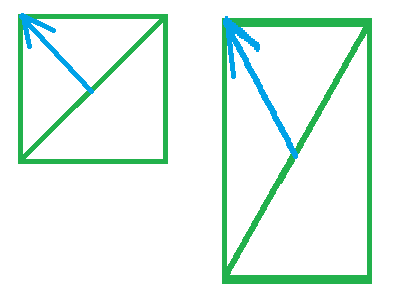
但是当不等比缩放的不同轴之间的差距很大时,这个效果就会更明显了.像下面这样:



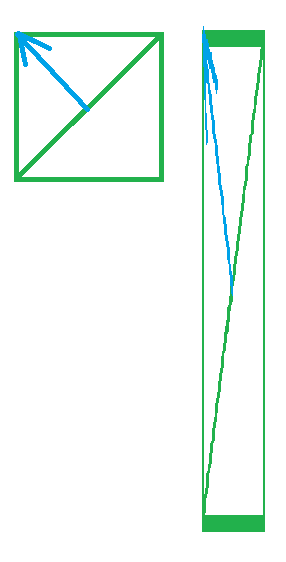
这个时候计算出来的光照就会和预期的有很明显的区别,给人很怪异的感觉了.

法线矩阵

这个时候,需要使用发现矩阵,其实就是模型矩阵逆矩阵的转置矩阵,用上效果立马就对了.

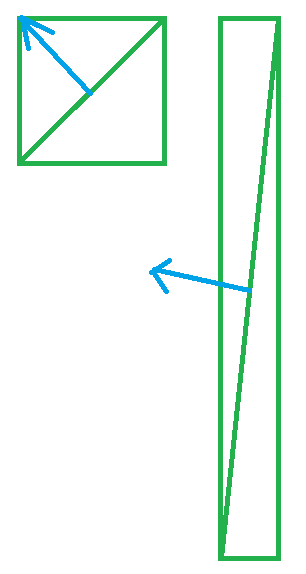
模型矩阵逆矩阵的转置矩阵作用原理

用法很简单,原理还是需要点时间来理解的.

首先我们的目标是法线最终需要与顶点的切线垂直.

定义:原法线为n,变换后法线为N,原来顶点处切线为t,变换后切线为T,模型矩阵为M,要计算的结果法线矩阵为X.

.表示点乘,表示矩阵乘以向量(也可以省略),或者向量间叉乘,`代表:

n . t = 0; //法线与切线垂直,所以点乘为0

N . T = 0; //最终结果亦垂直

N = X * n

T = M * t

将第三,四个方程带入第二个方程:

(X * n) . (M * t) = 0

点乘变换成叉乘

(X * n) . (M * t) => (X * n)^T * (M * t) => 省略* => (Xn)^T * Mt

=> n^TX^T * Mt

由于n . t = 0

X^TM = I

n . t = N . T = 0

X^TM = I => X = (M^-1)^T