【原】Coursera—Andrew Ng机器学习—课程笔记 Lecture 4_Linear Regression with Multiple Variables 多变量线性回归

Lecture 4 Linear Regression with Multiple Variables 多变量线性回归

4.1 多维特征 Multiple Features
4.2 多变量梯度下降 Gradient Descent for Multiple Variables
4.3 梯度下降法实践 1-特征缩放 Gradient Descent in Practice I - Feature Scaling
4.4 梯度下降法实践 2-学习率 Gradient Descent in Practice II - Learning Rate
4.5 特征和多项式回归 Features and Polynomial Regression
4.6 正规方程 Normal Equation
4.7 正规方程及不可逆性 Normal Equation Noninvertibility

4.1 多维特征 Multiple Features

　　参考视频: 4 - 1 - Multiple Features (8 min).mkv

　 Multivariate linear regression 多维线性回归

　　之前讨论单变量回归模型。现在讨论多变量模型，模型中的特征为（x1,x2,...,xn）。

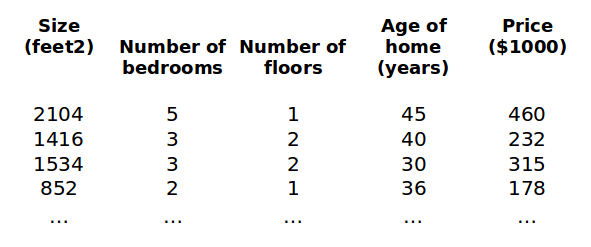
　　引入新的注释：

　　　　x⁽ⁱ⁾_j= value of feature j in the i^th training example　　特征矩阵中第 i 行的第 j 个特征，也就是第 i 个训练实例的第 j 个特征。

　　　　x⁽ⁱ⁾= the input (features) of the ith training example 　第 i 个训练实例，是特征矩阵中的第 i 行，是一个向量（vector）。

　　　　m = the number of training examples 　　　　　　　训练实例的个数

　　　　n = the number of features　　　　　　　　　　　　特征的数量

支持多变量的假设 h 表示为：

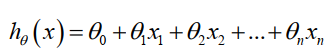
　　这个公式中有 n+1 个参数和 n 个变量，为了使得公式能够简化一些，引入 x⁰=1，则公式转化为：

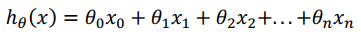
　　此时模型中的参数是一个 n+1 维的向量，任何一个训练实例也都是 n+1 维的向量，特征矩阵 X 的维度是 m * (n+1)。

公式可以简化为：

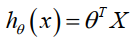
4.2 多变量梯度下降 Gradient Descent for Multiple Variables

参考视频: 4 - 2 - Gradient Descent for Multiple Variables (5 min).mkv

在具有多变量的线性回归中，定义代价函数 J(Θ) 如下：

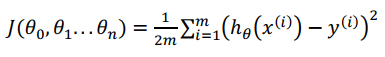
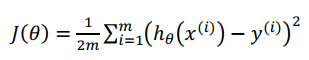
　　多变量线性回归模型如下。为了简化，我们加入X₀ = 1，参数Θ为一个n+1维向量vector。算法会同步更新每一个Θ_j（j = 0到n）

　　对比单变量梯度下降（左边）和多变量梯度下降（右边）。因为是我们引入的，其值为1，所以多变量梯度下降前两项 Θ₀ 和Θ₁和单变量梯度下降是一样的。

　　Python 代码：

def computeCost(X, y, theta):

　　inner = np.power(((X * theta.T) - y), 2)

　　return np.sum(inner) / (2 * len(X))

4.3 梯度下降法实践 1-特征缩放 Gradient Descent in Practice I - Feature Scaling

参考视频: 4 - 3 - Gradient Descent in Practice I - Feature Scaling (9 min).mkv

　　多维特征问题中，帮助梯度下降算法更快地收敛，特征需要具有相近的尺度（similar scale），这就需要我们进行 特征缩放Feature Scaling。
　　假设两个特征，房屋尺寸的值为 0-2000 平方英尺，而房间数量的值为 0-5，对应的代价函数等高线图会显得很扁（skewed elliptical shape），梯度下降算法需要非常多

次的迭代才能收敛（左图）。

　　把房屋尺寸除以2000，房屋数量除以5，尝试将所有特征的尺度都尽量缩放到 -1 到 1 之间，得到了近乎圆形的等高线（右图）。

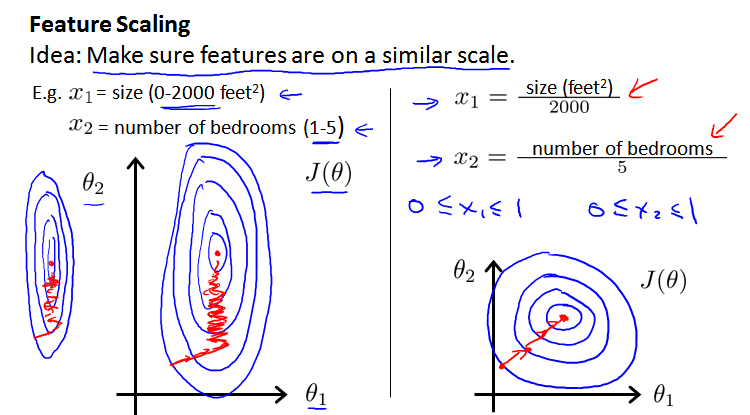
尺度也不是必须要 -1 到1，但是范围不能很大，也不能很小，例如：

　　最简单的方法是均值归一化 Mean normalization，令：

　　其中 μ_i是第 i 维所有取值的平均值。s_i是第 i 维取值的范围 range （或标准差 standard deviation）

4.4 梯度下降法实践 2-学习率 Gradient Descent in Practice II - Learning Rate

参考视频: 4 - 4 - Gradient Descent in Practice II - Learning Rate (9 min).mkv

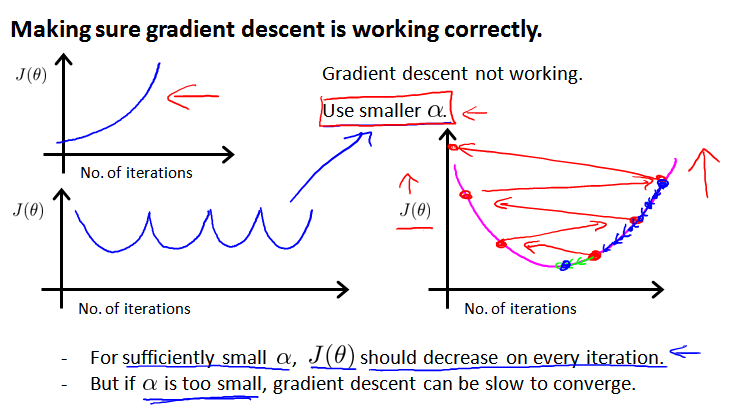
　为保证梯度下降算法正确运行，可以绘制迭代次数 iteration numbers 和代价函数的图表，观测算法在何时趋于收敛（左边）。

　　还有一些自动测试是否收敛的方法 automatic convergence test，例如使用阈值 ε（右边）。因为阈值的大小很难选取，还是左侧的图表比较好。

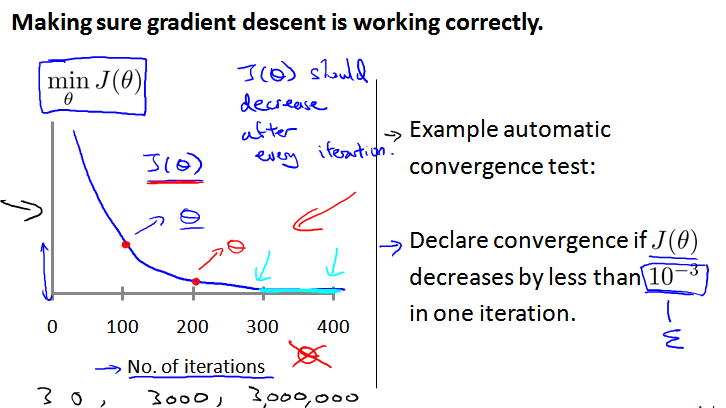
　　随着迭代次数增加，代价函数应该呈下降趋势。如果上升或者频繁升降，说明 α 取得太大，可能导致不能收敛。如果 α 取值太小，算法会运行的很慢，但还是下降的，通常会迭代很多次后收敛。

　　学习率可以尝试如下值：

4.5 特征和多项式回归 Features and Polynomial Regression

　　参考视频: 4 - 5 - Features and Polynomial Regression (8 min).mkv

4.5.1 创造新的特征

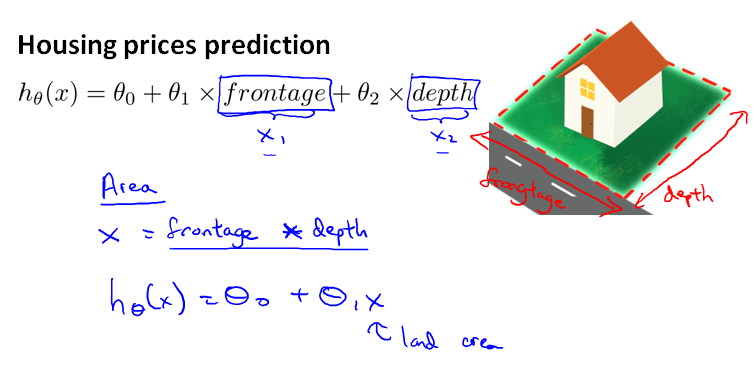
　　不一定非要用已有特征，可以创造新的特征，例如：面积 = 长 * 宽。这时二次函数变成了单变量函数。

4.5.2 多项式回归 Polynomial Regression

　　二次方程模型：

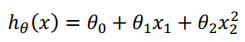
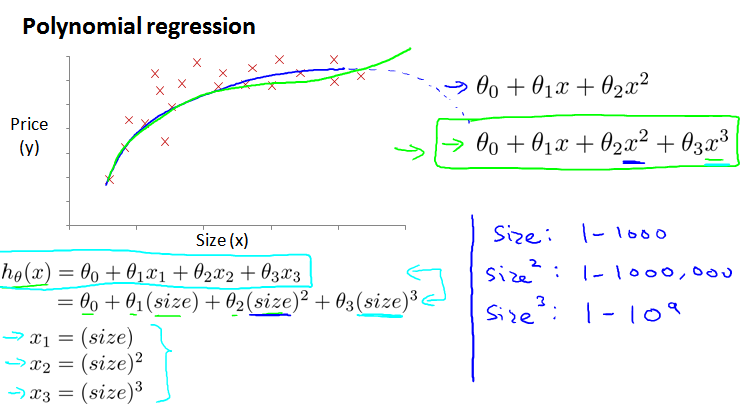
　　三次方程模型：

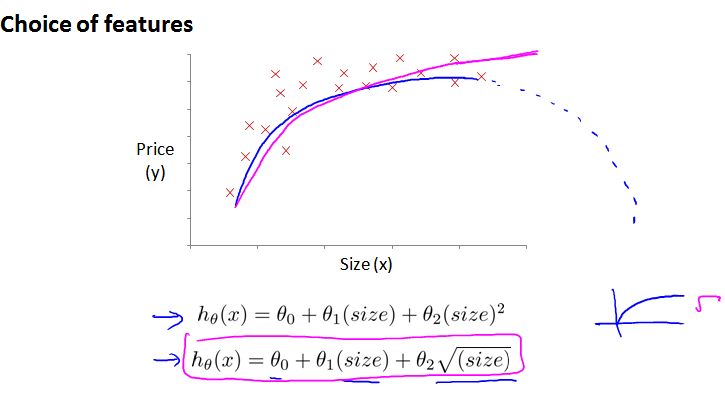
　　因为实际生活中，随着房屋面积上升、房价不可能减小，而二次曲线会先上升后下降。选择三次方模型，引入另外的变量替换高次幂，将其转换为线性回归模型。

　　为了和曲线拟合的更好，还可以使用 平方根 square root

4.6 正规方程 Normal Equation

参考视频: 4 - 6 - Normal Equation (16 min).mkv

4.6.1 正规方程 Normal Equation

正规方程的思想：假设代价函数 J(Θ) 的偏导数等于0，求解方程，得到使代价函数 J(Θ) 最小的参数 Θ。即求曲线的最低点（切线斜率为0）。

最简单的情况，只有一维，代价函数是二次曲线：

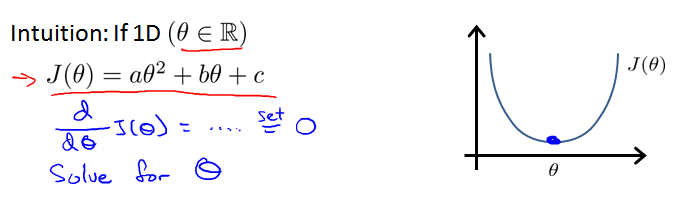
如果有n个特征，则 Θ 为n+1维。针对代价函数 J(Θ) 的每一项 J(Θ_j) ，设其偏导数为0。通过数学方法求解方程，得到使代价函数 J(Θj) 最小的 Θj。

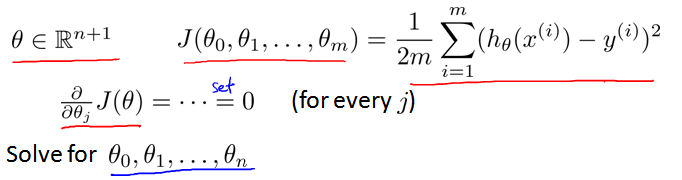
4.6.2 正规方程的解

假设训练集特征矩阵为 X（包含x₀ = 1），结果为向量y，则解Θ可以通过公式求出：

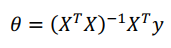
　　例子，四个数据：

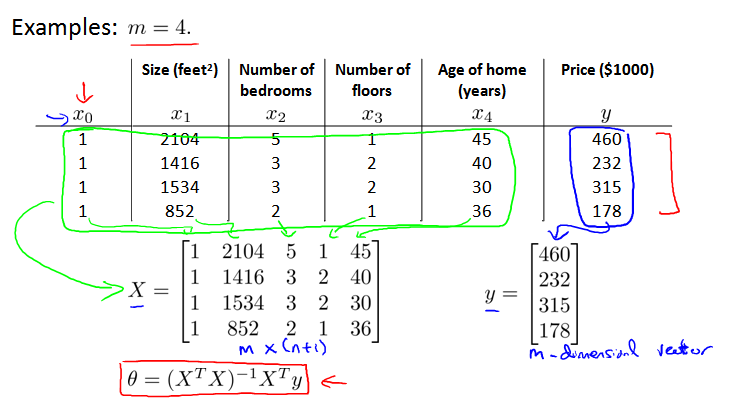
解 Θ 为：

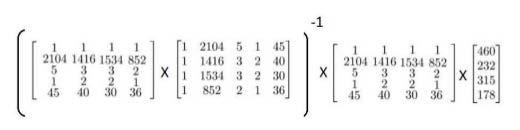
　　正规方程方法中，不用进行特征缩放 Feature Scaling。

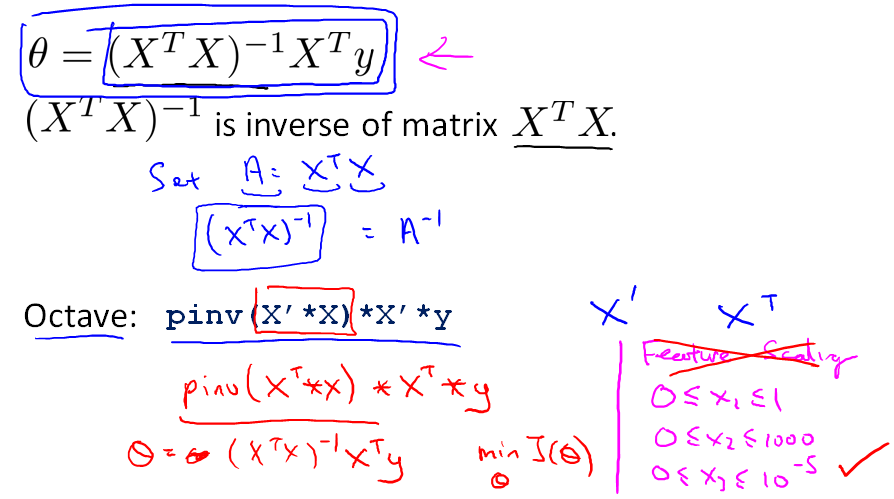
　　在Octave 中，求解的代码为：

1 pinv( X' * X ) * X' * y

4.6.3 梯度下降和正规方程的比较

　　1、梯度下降需要选择学习率 α，迭代很多步，正规方程只需要一步。

　　2、正规方程依赖于矩阵计算。由于计算逆矩阵的时间复杂度是 O(n³)，当n比较大时，计算过程会特别慢

　　总结：

　　 1、特征变量的数目 n 不大的时候，推荐使用正规方程。

　　2、n 比较大的时候（例如10000），考虑梯度下降。

　　 3、某些算法（例如分类算法中的逻辑回归）不能使用正规方程法，只能使用梯度下降。

　　正规方程的python实现：

 import numpy as np

 def normalEqn(X, y):

     theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X 等价于 X.T.dot(X)

     return theta

4.7 正规方程及不可逆性 Normal Equation Noninvertibility

参考视频: 4 - 7 - Normal Equation Noninvertibility (Optional) (6 min).mkv

当矩阵XTX不可逆怎么办？不可逆的问题很少发生，即使发生，使用pinv()也能正常算出结果。

pinv() pseudo-inverse伪逆即使 singular degenerate 也能算出来逆矩阵

inv() 　 inverse逆　　　　　引入了先进的数值计算的概念

　　两种情况可能导致不可逆：

1、有冗余特征 redundant features，即特征值线性相关（例如 x₁ = 常数 * x₂）

　　解决：删除冗余特征

2、特征维数 n ≤ 数据规模 m （例如10个样本适应100+1个参数）

　　解决：删除特征，或者使用线性代数中的正则化 regularization方法