利用道格拉斯·普客法（DP法）压缩矢量多边形（C++）

1.算法描述

经典的Douglas-Peucker算法（简称DP法）描述如下：

（1）在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；

（2）得到曲线上离该直线段距离最大的点C，计算其与AB的距离d；

（3）比较该距离与预先给定的阈值threshold的大小，如果小于threshold，则该直线段作为曲线的近似，该段曲线处理完毕。

（4）如果距离大于阈值，则用C将曲线分为两段AC和BC，并分别对两段取信进行1~3的处理。

（5）当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似

2.算法分析

①显然，整个过程是一个迭代过程，第四步时迭代，再次回到第一步。

②由于计算开方耗时，所以直接取d²作为评判值更加方便。

③DP法一般是化简一条曲线，本次化简的是多边形，实质是一条首尾相连的多边形，意味着曲线首尾两点的坐标相等。如果两点坐标相等，则第二步计算距离时会出现分母为0的问题。因此要换一个就近的点。

3.算法实现

①计算某点到已知两点的距离。

// 计算一点到一条直线（已知两点）的距离
double disP2L(CMyPoint* first, CMyPoint* last, CMyPoint* third) //first和last分别为线的两端，third是第三点
																//CMyPoint是点的类型，可以换成CPoint
{
	double x0 = first->Getx();
	double y0 = first->Gety();
	double x1 = last->Getx();
	double y1 = last->Gety();
	double x = third->Getx();
	double y = third->Gety();
	//diSquare是d²，不开方，耗时更短。
	double disSuqare = ((y0 - y1)*x + (x1 - x0)*y + (x0*y1 - x1*y0))*((y0 - y1)*x + (x1 - x0)*y + (x0*y1 - x1*y0)) / ((x1 - x0)*(x1 - x0) + (y1 - y0)*(y1 - y0));
	return disSuqare;
}

②压缩算法

// Douglas–Peucker法，20190220，压缩，zf
void DP(vector<CMyPoint*> inputLine)        //输入是包含指针的数组，vector类型
{
	if (inputLine.size() <= 2)              //若少于两点，直接返回
		return;
	int size = inputLine.size();
	CMyPoint *first = inputLine[0];         //定义首点
	CMyPoint *last = inputLine[size - 1];   //定义尾点
	while (last->Getx() == first->Getx() && last->Gety() == first->Gety()) {//若首尾相同，则换点
		size = size - 1;
		last = inputLine[size - 1];
	}
	int flag = 0;                            //标记距离最大的点的下标
	double disSquare = 0;
	for (int i = 1; i<inputLine.size() - 1; i++) {
		double temp = disP2L(first, last, inputLine[i]);
		if (temp>disSquare) {                //记录最大距离及编号
			disSquare = temp;
			flag = i;
		}
	}
	if (disSquare<4) {                       //判断值与阈值的关系,阈值自己设定
		out_DP.push_back(first);             //如果小于阈值，则保留首尾点
		out_DP.push_back(last);              //out_DP是一个全局变量，vector<CMyPoint*> out_DP
		                                     //用于存储留下来的点,是最后的成果
	}
	else {                                   //否则分成两段
		vector<CMyPoint*> head, rear;
		for (int j = 0; j<inputLine.size(); j++) {
			if (j <= flag) head.push_back(inputLine[j]);
			if (j >= flag) rear.push_back(inputLine[j]);
		}
		DP(head);                            //迭代进行
		DP(rear);
	}
}

4.实验效果

分别是前、后

  

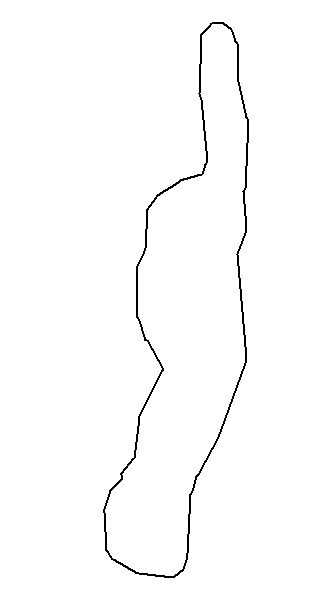
在保持图形和面积基本不变的前提下，多边形的点变少，压缩具有较好效果。