欧拉函数(Euler_Function)

一、基本概述
在数论，对正整数n，欧拉函数varphi(n)是少于或等于n的数中与n互质的数的数目。此函数以其首名研究者欧拉命名，它又称为Euler's totient function、φ函数、欧拉商数等。

二、计算公式

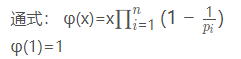
三、基本性质
欧拉函数用希腊字母φ表示,φ(N)表示N的欧拉函数.

对φ(N)的值,我们可以通俗地理解为小于N且与N互质的数的个数(包含1).

欧拉函数的一些性质:

1.对于素数p, φ(p)=p-1，对于对两个素数p,q φ（pq）=pq-1

欧拉函数是积性函数,但不是完全积性函数.

证明：

函数的积性即：若m,n互质,则φ(mn)=φ(m)φ(n).由“m,n互质”可知m,n无公因数,所以φ(m)φ(n)=m(1-1/p1)(1-1/p2)(1-1/p3)…(1-1/pn)·n(1-1/p1')(1-1/p2')(1-1/p3')…(1-1/pn'),其中p1,p2,p3...pn为m的质因数,p1',p2',p3'...pn'为n的质因数,而m,n无公因数,所以p1,p2,p3...pn,p1',p2',p3'...pn'互不相同,所以p1,p2,p3...pn,p1',p2',p3'...pn'均为mn的质因数且为mn质因数的全集,所以φ(mn)=mn(1-1/p1)(1-1/p2)(1-1/p3)…(1-1/pn)(1-1/p1')(1-1/p2')(1-1/p3')…(1-1/pn'),所以φ(mn)=φ(m)φ(n).

即φ(mn)=φ(n)*φ(m)只在(n,m)=1时成立.

2.对于一个正整数N的素数幂分解N=P1^q1*P2^q2*...*Pn^qn.

φ(N)=N*(1-1/P1)*(1-1/P2)*...*(1-1/Pn).

3.除了N=2,φ(N)都是偶数.

4.设N为正整数,∑φ(d)=N (d|N).

四、求欧拉函数
1、埃拉托斯特尼筛求欧拉函数

观察欧拉函数的公式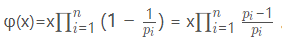， 。我们用phi[x]表示φ(x)。可以一开始把phi[x]赋值为x，然后每次找到它的质因数就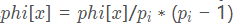（先除再乘，避免溢出）。当然，若只要求一个数的欧拉函数，可以从1到sqrt(n)扫一遍，若gcd(i,n)=1就更新phi[n] phi[n]phi[n]。复杂度为O(logn)（代码就不给了）。那要求1~n所有数的欧拉函数呢？可以用埃拉托斯特尼筛的思想，每次找到一个质数，就把它的倍数更新掉。这个复杂度虽然不是O(n)，但还是挺快的（据说是O(n*ln ln n)，关于证明，可以点这里，虽然我看不懂）。
代码如下：

void euler(int n)
{
    for (int i=;i<=n;i++) phi[i]=i;
    for (int i=;i<=n;i++)
    {
        if (phi[i]==i)//这代表i是质数
        {
            for (int j=i;j<=n;j+=i)
            {
                phi[j]=phi[j]/i*(i-);//把i的倍数更新掉
            }
        }
    }
}
 

2、欧拉筛求欧拉函数

前提是要懂欧拉筛。每个数被最小的因子筛掉的同时，再进行判断。i表示当前做到的这个数，prime[j]表示当前做到的质数，那要被筛掉的合数就是i*prime[j]。若prime[j]在这个合数里只出现一次（i%prime[j]!=0），也就是i和prime[j]互质时，则根据欧拉函数的积性函数的性质，phi[i * prime[j]]=phi[i] * phi[prime[j]]。若prime[j]在这个合数里出现了不止一次（i%prime[j]=0），也就是这个合数的所有质因子都在i里出现过，那么根据公式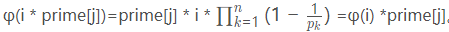，复杂度为O(n)。

还是看代码吧：

void euler(int n)
{
    phi[]=;//1要特判
    for (int i=;i<=n;i++)
    {
        if (flag[i]==)//这代表i是质数
        {
            prime[++num]=i;
            phi[i]=i-;
        }
        for (int j=;j<=num&&prime[j]*i<=n;j++)//经典的欧拉筛写法
        {
            flag[i*prime[j]]=;//先把这个合数标记掉
            if (i%prime[j]==)
            {
                phi[i*prime[j]]=phi[i]*prime[j];//若prime[j]是i的质因子，则根据计算公式，i已经包括i*prime[j]的所有质因子
                break;//经典欧拉筛的核心语句，这样能保证每个数只会被自己最小的因子筛掉一次
            }
            else phi[i*prime[j]]=phi[i]*phi[prime[j]];//利用了欧拉函数是个积性函数的性质
        }
    }
}

五、例题

http://acm.hdu.edu.cn/showproblem.php?pid=2588

http://poj.org/problem?id=2480

http://acm.hdu.edu.cn/showproblem.php?pid=3501

https://www.luogu.org/problemnew/show/P2158