P5752 [NOI1999] 棋盘分割题解

本文来自我的洛谷博客。

这个题解思路虽然与其他人的思路相同，

但力求使用清晰易懂的图片和文字，讲解最简洁的道理。

请大家耐心地看完，注意要结合图片一起哦~~

2022-8-24 更改了格式与错别字。

2022-8-28 更改了数学公式格式。

这是本蒟蒻第一次写题解，不足之处请多包涵。

---

题目大意：

读完题的可以跳过这一部分。

给定一个矩阵，每个位置上都有数字。

可以分割 \(n-1\) 次，每次分割为 \(2\) 个矩形，然后把一半放在一旁，然后在另外一半继续割。

像这样：

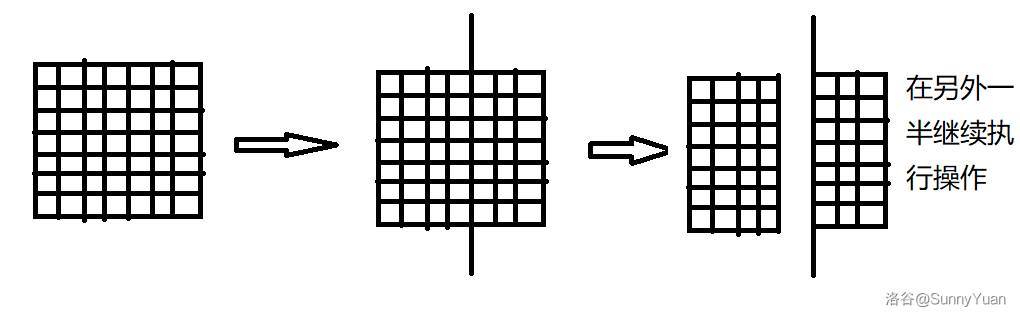
可以横切也可以纵切。

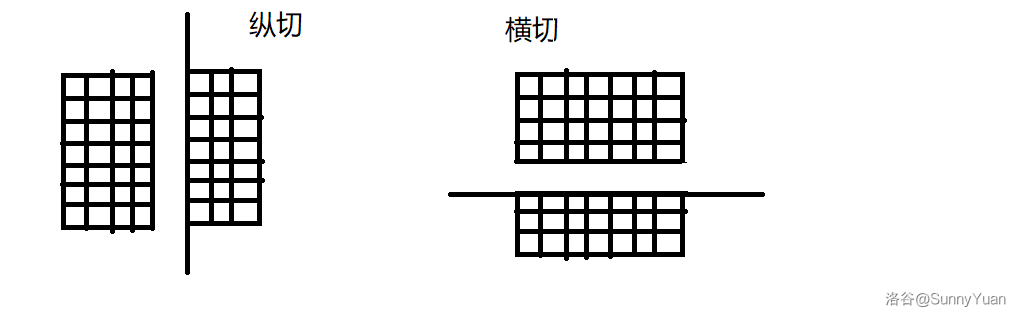
样例给的很好。

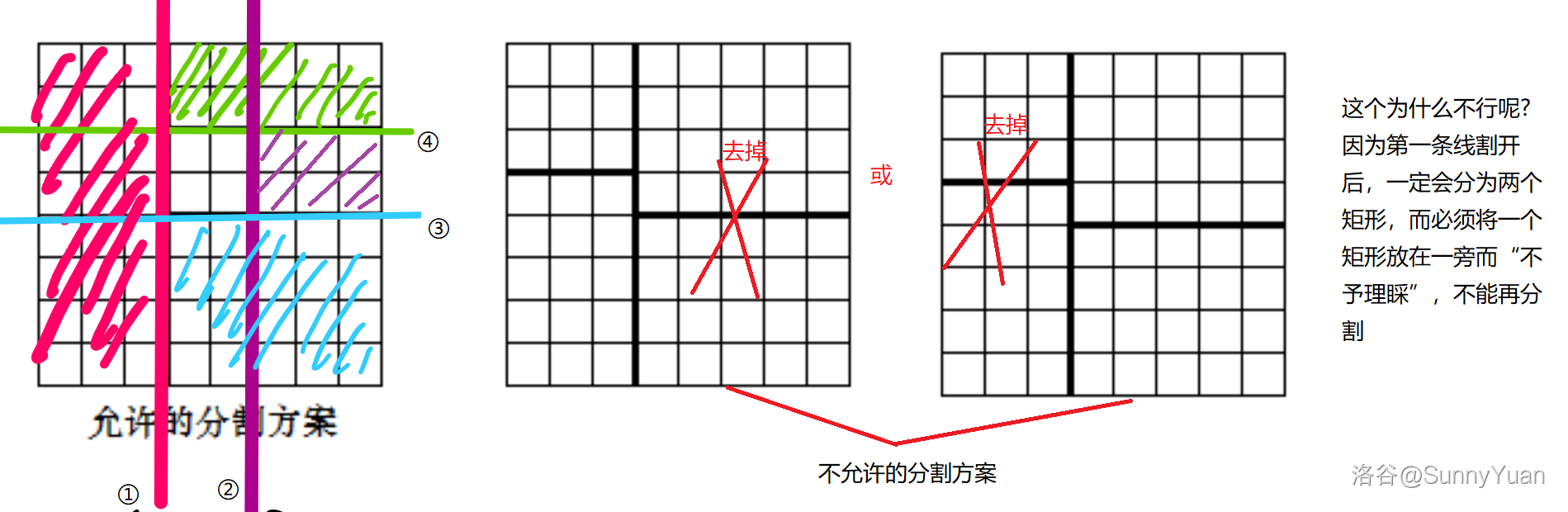
然后就分为 \(n\) 块（因为割了 \(n-1\) 次）。

记 \(X=\dfrac{s}{n}\)，\(s\) 为矩阵中所有的数字之和。

设第 \(i\) 块的和为 \(x_i\)，那么求出怎样割才能使 $\sum_{i=1}^{n}(x_i-X)2 $ 更小。

---

分析问题：

我们看到这种分割问题，最后组合起来求总体最优值，便可以立马联想到区间 DP。这叫望梅止渴做 DP 问题的复杂反射。

毕竟区间 DP 的主要思想就是大区间包含小区间，

小区间汇集成大区间。

好了，废话不多说，我们先从如下几个角度思考：

• 状态表示
• 状态含义
• 目标状态
• 状态转移

一、状态表示：\(f(x1,y1,x2,y2,k)\)。

二、状态含义：\(f(x1,y1,x2,y2,k)\) 表示求解子矩阵 \((x1,y1)\sim(x2,y2)\) 割了 \(k\) 刀得来的最优解（即下图框住区域的最优解）。

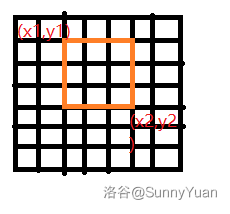
三、目标状态：\(f(1,1,8,8,n)\)，即求解整个矩阵被割了 \(n\) 刀的最优解。

四、状态转移：

我们以下图为例，讲解 \(f(x1,y1,x2,y2,k)\) 是如何被拆分的。

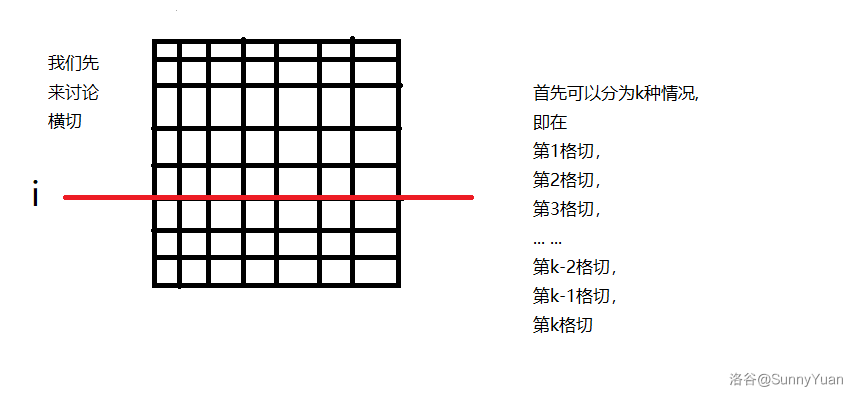
①：考虑选择上面继续割（如下图），丢掉下面的，其分界线为第 \(i\) 行。

所以应该取上面的最优值，同时少割一刀：\(f(x1,y1,i,y2,k-1)\)，

而下面的部分为定值：\(\dfrac{(sum-X)^2}{n}\)。

\(sum\) 为下面的部分所有格子的和。

这两个部分合起来就是 \(f(x1,y1,x2,y2,k)\)。

---

②：考虑选择下面继续割（如上图）。

上面部分的定值：\(\dfrac{(sum-X)^2}{n}\)。

下面的最优值：\(f(i+1,y1,x2,y2,k-1)\)。

\(sum\) 为上面的部分所有格子的和。

---

下面考虑纵切。

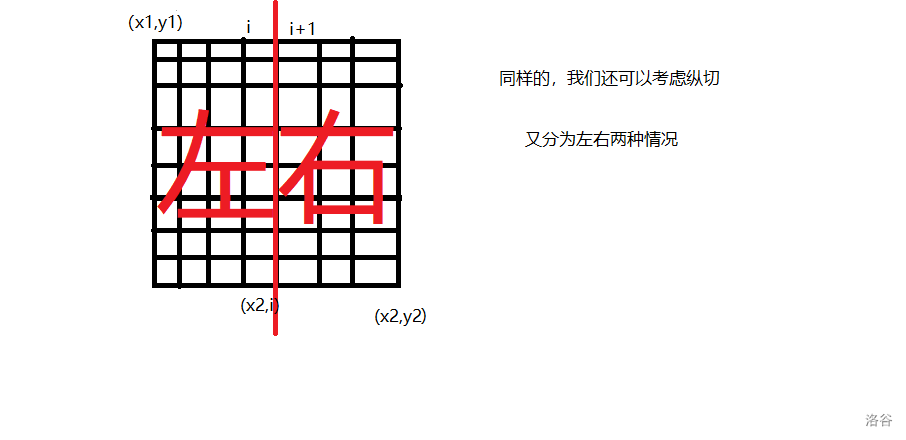
③：考虑选择左边继续割（如上图），分界线为第 \(i\) 列。

取左边的最优值：\(f(x1,y1,x2,i,k-1)\)，

右边的部分为定值：\(\dfrac{(sum-X)^2}{n}\)。

\(sum\) 为右边的部分所有格子的和。

---

④：考虑选择右边继续割（如上图）。

取右边的最优值：\(f(x1,i+1,x2,y2,k-1)\)，

左边的部分为定值：\((sum-X)\times(sum-X)/n\)，

\(sum\) 为左边的部分所有格子的和。

---

我们每次取一个值，其实都是在将问题规模缩小。

情况考虑清楚了，那怎么从一个 \(f\) 到另一个 \(f\) 呢，如果是用普通的区间 DP，那估计要使用 \(5\) 层甚至更多的循环，所以，我们使用万能的记忆化搜索，免去繁琐的循环结构。

---

综上所述，

我们便实现了对大区间的拆分。

而我们不断提到 \(sum\)，是一块区域的和，那么，我们可以使用二维前缀和来维护。相信大家一定会。

好了，上 AC 代码。

#include <bits/stdc++.h>

using namespace std;

const int N=15;
const double INF=1e10;				//因为要求min,所以要定义INF

int n;
int m=8;
double X;							//平均值
double s[N][N];						//记录每个格子的值
double f[N][N][N][N][N];			//状态

double GetSum(int x1,int y1,int x2,int y2)//求[x1,y1]~[x2,y2]的和,为下文的GetX服务
{
    return s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
}

double GetX(int x1,int y1,int x2,int y2)// 计算上文的(sum−X)×(sum−X)/n。
{
    return (GetSum(x1,y1,x2,y2)-X)*(GetSum(x1,y1,x2,y2)-X)/n;
}

double DFS(int x1,int y1,int x2,int y2,int k)//使用记忆化搜索进行递归调用
{
    double& v=f[x1][y1][x2][y2][k];//因为太难写了，所以给f[x1][y1][x2][y2][k]建立引用
    if(v>=0)return v;				//已经访问过该点了，直接返回
    if(k==1)return v=GetX(x1,y1,x2,y2);//最后一块，不可能再割了

    v=INF;							//为求最小值做准备

    for(int i=x1;i<x2;i++)			//下面是刚刚讨论的结果
    {
        v=min(v,DFS(x1,y1,i,y2,k-1)+GetX(i+1,y1,x2,y2));
        v=min(v,DFS(i+1,y1,x2,y2,k-1)+GetX(x1,y1,i,y2));
    }

    for(int i=y1;i<y2;i++)
    {
        v=min(v,DFS(x1,y1,x2,i,k-1)+GetX(x1,i+1,x2,y2));
        v=min(v,DFS(x1,i+1,x2,y2,k-1)+GetX(x1,y1,x2,i));
    }

    return v;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=m;j++)
        {
            double x;
            scanf("%lf",&x);
            s[i][j]=s[i-1][j]+s[i][j-1]+x-s[i-1][j-1];						//建立前缀和
        }
    }
    X=s[m][m]/n;					//求平均值
    memset(f,0x80,sizeof f);		//初始化
    printf("%.3f\n",sqrt(DFS(1,1,m,m,n)));//注意，一定要根号啊啊啊!!!
    return 0;
}