迪杰斯特拉Dijkstra算法介绍
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。
然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 ... 重复该操作,直到遍历完所有顶点。
操作步骤
(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
单纯的看上面的理论可能比较难以理解,下面通过实例来对该算法进行说明。
迪杰斯特拉算法图解

以上图G4为例,来对迪杰斯特拉进行算法演示(以第4个顶点D为起点)。

初始状态:S是已计算出最短路径的顶点集合,U是未计算除最短路径的顶点的集合!
第1步:将顶点D加入到S中。
此时,S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。
第2步:将顶点C加入到S中。
上一步操作之后,U中顶点C到起点D的距离最短;因此,将C加入到S中,同时更新U中顶点的距离。以顶点F为例,之前F到D的距离为∞;但是将C加入到S之后,F到D的距离为9=(F,C)+(C,D)。
此时,S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。
第3步:将顶点E加入到S中。
上一步操作之后,U中顶点E到起点D的距离最短;因此,将E加入到S中,同时更新U中顶点的距离。还是以顶点F为例,之前F到D的距离为9;但是将E加入到S之后,F到D的距离为6=(F,E)+(E,D)。
此时,S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。
第4步:将顶点F加入到S中。
此时,S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。
第5步:将顶点G加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。
第6步:将顶点B加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。
第7步:将顶点A加入到S中。
此时,S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。
此时,起点D到各个顶点的最短距离就计算出来了:A(22) B(13) C(3) D(0) E(4) F(6) G(12)。
迪杰斯特拉算法的代码说明
以"邻接矩阵"为例对迪杰斯特拉算法进行说明,对于"邻接表"实现的图在后面会给出相应的源码。
1. 基本定义

// 邻接矩阵
typedef struct _graph
{
char vexs[MAX]; // 顶点集合
int vexnum; // 顶点数
int edgnum; // 边数
int matrix[MAX][MAX]; // 邻接矩阵
}Graph, *PGraph; // 边的结构体
typedef struct _EdgeData
{
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
}EData;

Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
EData是邻接矩阵边对应的结构体。
2. 迪杰斯特拉算法

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
#define MAX 100
#define INF (~(0x1<<31))
typedef struct Graph
{
char vexs[MAX];
int vexnum;
int edgnum;
int matrix[MAX][MAX];
} Graph,*PGraph; typedef struct EdgeData
{
char start;
char end;
int weight;
} EData; static int get_position(Graph g,char ch)
{
int i;
for(i=0; i<g.vexnum; i++)
if(g.vexs[i]==ch)
return i;
return -1;
} Graph* create_graph()
{
char vexs[]= {'A','B','C','D','E','F','G'};
int matrix[][7]=
{
{0,12,INF,INF,INF,16,14},
{12,0,10,INF,INF,7,INF},
{INF,10,0,3,5,6,INF},
{INF,INF,3,0,4,INF,INF},
{INF,INF,5,4,0,INF,8},
{16,7,6,INF,2,0,9},
{14,INF,INF,INF,8,9,0}
};
int vlen=sizeof(vexs)/sizeof(vexs[0]);
int i,j;
Graph *pG;
if((pG=(Graph*)malloc(sizeof(Graph)))==NULL)
return NULL;
memset(pG,0,sizeof(pG));
pG->vexnum=vlen;
for(i=0; i<pG->vexnum; i++)
pG->vexs[i]=vexs[i];
for(i=0; i<pG->vexnum; i++)
for(j=0; j<pG->vexnum; j++)
pG->matrix[i][j]=matrix[i][j];
for(i=0; i<pG->vexnum; i++)
{
for(j=0; j<pG->vexnum; j++)
{
if(i!=j&&pG->matrix[i][j]!=INF)
pG->edgnum++;
}
}
pG->edgnum/=2;
return pG;
} void print_graph(Graph G)
{
int i,j;
printf("Matrix Graph: \n");
for(i=0; i<G.vexnum; i++)
{
for(j=0; j<G.vexnum; j++)
printf("%10d ",G.matrix[i][j]);
printf("\n");
}
} EData* get_edges(Graph G)
{
EData *edges;
edges=(EData*)malloc(G.edgnum*sizeof(EData));
int i,j;
int index=0;
for(i=0; i<G.vexnum; i++)
{
for(j=i+1; j<G.vexnum; j++)
{
if(G.matrix[i][j]!=INF)
{
edges[index].start=G.vexs[i];
edges[index].end=G.vexs[j];
edges[index].weight=G.matrix[i][j];
index++;
}
}
}
return edges;
} void dijkstra(Graph G,int vs,int prev[],int dist[])
{
int i,j,k;
int min;
int tmp;
int flag[MAX]; for(i=0;i<G.vexnum;i++)
{
flag[i]=0;
prev[i]=vs;
dist[i]=G.matrix[vs][i];
} flag[vs]=1;
dist[vs]=0; for(i=1;i<G.vexnum;i++)
{
min=INF;
for(j=0;j<G.vexnum;j++)
{
if(flag[j]==0&&dist[j]<min)
{
min=dist[j];
k=j;
}
}
flag[k]=1;
for(j=0;j<G.vexnum;j++)
{
tmp=((G.matrix[k][j]==INF)?INF:(min+G.matrix[k][j]));
if(flag[j]==0&&tmp<dist[j])
{
dist[j]=tmp;
prev[j]=k;
}
}
}
printf("dijktra(%c):\n",G.vexs[vs]);
for(i=0;i<G.vexnum;i++)
printf(" shortest (%c,%c)=%d\n",G.vexs[vs],G.vexs[i],dist[i]);
} int main()
{
Graph *pG;
pG=create_graph();
print_graph(*pG);
int prev[MAX];
int dist[MAX];
dijkstra(*pG,3,prev,dist);
int i;
for(i=0;i<pG->vexnum;i++)
printf("%c %c \n",pG->vexs[prev[i]],pG->vexs[i]);
}

运行结果:
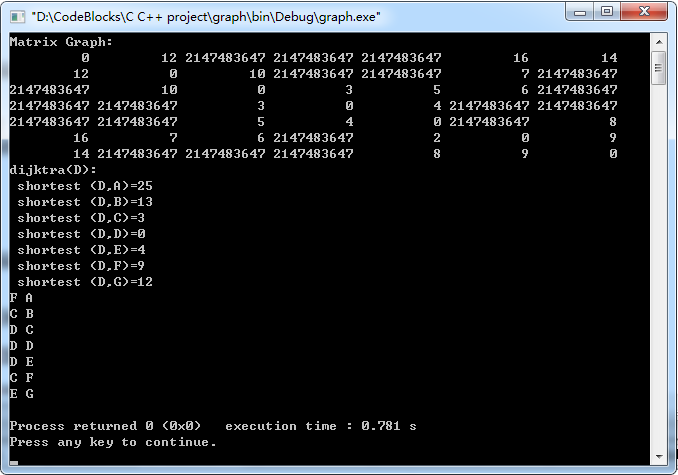
迪杰斯特拉Dijkstra算法介绍的更多相关文章
- JS实现最短路径之迪杰斯特拉(Dijkstra)算法
最短路径: 对于网图来说,最短路径是指两个顶点之间经过的边上权值和最少的路径,我们称第一个顶点是源点,最后一个顶点是终点 迪杰斯特拉 ( Dijkstra) 算法是并不是一下子就求出 了 Vo 到V8 ...
- 最短路径算法-迪杰斯特拉(Dijkstra)算法在c#中的实现和生产应用
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径. 它的主要特点是以起始点为中心向外层层扩展(广度优先遍历思想),直到扩展到终点为止 贪心算法(Greedy ...
- 最短路径-迪杰斯特拉(dijkstra)算法及优化详解
简介: dijkstra算法解决图论中源点到任意一点的最短路径. 算法思想: 算法特点: dijkstra算法解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树.该算法常用于路由算 ...
- 单源最短路径算法:迪杰斯特拉 (Dijkstra) 算法(一)
一.算法介绍 迪杰斯特拉算法(英语:Dijkstra's algorithm)由荷兰计算机科学家艾兹赫尔·迪杰斯特拉在1956年提出.迪杰斯特拉算法使用了广度优先搜索解决赋权有向图的单源最短路径问题. ...
- C# 迪杰斯特拉(Dijkstra)算法
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径.主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止. 其基本思想是,设置顶点集合S并不断地作 ...
- 最短路径 - 迪杰斯特拉(Dijkstra)算法
对于网图来说,最短路径,是指两顶点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点为源点,最后一个顶点为终点.最短路径的算法主要有迪杰斯特拉(Dijkstra)算法和弗洛伊德(Floyd ...
- 图的最短路径---迪杰斯特拉(Dijkstra)算法浅析
什么是最短路径 在网图和非网图中,最短路径的含义是不一样的.对于非网图没有边上的权值,所谓的最短路径,其实就是指两顶点之间经过的边数最少的路径. 对于网图,最短路径就是指两顶点之间经过的边上权值之和最 ...
- 单源最短路径算法:迪杰斯特拉 (Dijkstra) 算法(二)
一.基于邻接表的Dijkstra算法 如前一篇文章所述,在 Dijkstra 的算法中,维护了两组,一组包含已经包含在最短路径树中的顶点列表,另一组包含尚未包含的顶点.使用邻接表表示,可以使用 BFS ...
- 迪杰斯特拉(Dijkstra)算法
# include <stdio.h> # define MAX_VERTEXES //最大顶点数 # define INFINITY ;//代表∞ typedef struct {/* ...
随机推荐
- eclipse 使用Maven deploy命令部署构建到Nexus上 【二】
http://blog.csdn.net/jun55xiu/article/details/43051627
- android 多线程概述
android多线程,一直是一个麻烦的事情,要掌握它的本质,我们需要搞清楚一个问题,linux多线程的本质. 我们这篇文章,来讨论以下的议程: 了解linux的历程,了解android的异步任务机制, ...
- isPostback 的原理及作用(很easy)
1.IsPostBack用来推断表单是否是回发. (不是第一次请求),是点击表单的提交button回发过来的.是否是回发与get请求还是Post请求无关.可是普通情况下回发都是Post请求. 一般Ge ...
- 初探 hexo博客
近期两天迷上了hexo和gitcafe.最终搭建好了自己的个人主页.以后也能够用那个来写博客啦~直接用的gitcafe的二级域名和server,(gitcafe的server在国外.速度也挺快的),h ...
- 将浮点数保持几位小数,尾数舍入的Format函数
select format(hours,2) from pos.daywork
- C语言高速入门系列(二)
C语言高速入门系列(二) -----转载请注明出处coder-pig 本节引言: 在前面一节中我们对C语言进行了初步的了解,学会了使用IDE进行代码的编写,编译执行! 在这一节中我们会对C语言的基本的 ...
- Failed to fetch URL https://dl-ssl.google.com/android/repository/repository-6.xml, reason: Connection to https://dl-ssl.google.com refused
修改hosts文件.文件在C:\WINDOWS\system32\drivers\etc目录下,Linux用户打开/etc/hosts文件.用记事本打开文件后添加以下内容. #Google主页203. ...
- PyQt5教程——事件和信号(5)
PyQt5中的事件和信号 在这部分PyQt5编程教程中,我们探索应用中事件和信号的发生. 事件 所有的GUI应用都是事件驱动的.事件主要由应用的用户操作产生的.但是事件可能由其他条件触发,比如:一个网 ...
- Linux学习笔记——Ubuntu更新软件源
0.前言 通过改动ubuntu软件源可提高apt命令下载安装软件的速度. 參考资料 [官方资料]--配置文件改动方法 [Ubuntu如何改动软件源地址]--使用ubun ...
- tar 归档中找不到
今天在解压tar.gz包时遇到的错误: 刚开始以为是路径的问题,然后感觉是tar.gz包的问题,后来查了一下才知道,记录一下: 一定要加上那个-C 参数表示更换目录的意识 -C --dire ...
