【机器学习】--Adaboost从初始到应用
一、前述
AdaBoost算法和GBDT(Gradient Boost Decision Tree,梯度提升决策树)算法是基于Boosting思想的机器学习算法。在Boosting思想中是通过对样本进行不同的赋值,对错误学习的样本的权重设置的较大,这样,在后续的学习中集中处理难学的样本,最终得到一系列的预测结果,每个预测结果有一个权重,较大的权重表示该预测效果较好。
二、具体原理
AdaBoost,是英文"Adaptive Boosting"(自适应増强)的缩写,由Yoav Freund和Robert Schapire在1995年提出。它的自适应在于:前一个基本分器分错的样本会得到加强,加权后的全体样本再次被用来训练、下一个基本分类器。同时,在每一轮中加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。
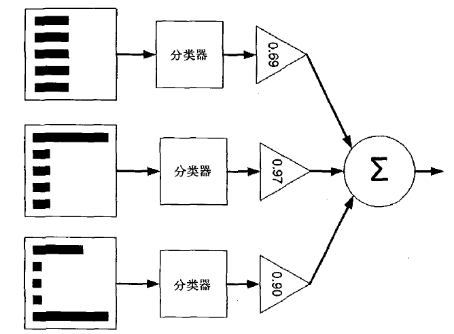
1、算法过程
1. 初始化训练数据的权值分布。如果有 N 个样本,则每一个训练样本最开始时都被赋予相同的权重:1/ N
2. 训练弱分类器。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权重就被降低;相反,如果某个样本点没有被准确地分类,那么它的权重就得到提高。然后,权重更新过的样本集被用于训练下一个类器,整个训练过程如此迭代地进行下去。
3. 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。换言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
2、具体过程
给定一个训练数据集 T ={( x 1, y 1), ( x 2, y 2)...( xN , yN )},其中实例 ;r e 义, yi 属于标记集合{-1, + 1}, Adaboost 的目的就是从训练数据中学习一系列弱分类器或基本分类器,然后从这些弱分类器组合成一个强分类器。
Adaboost 的算法流程如下:



三、案例分析
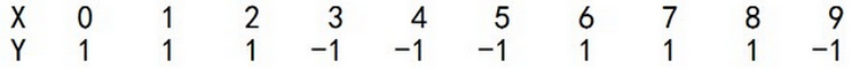

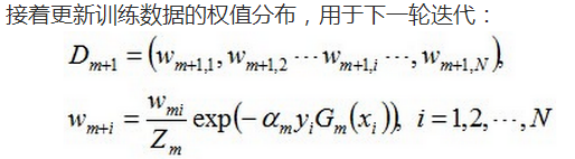




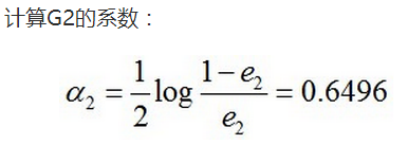
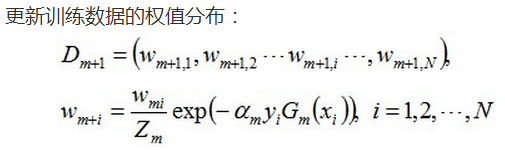
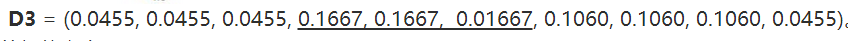
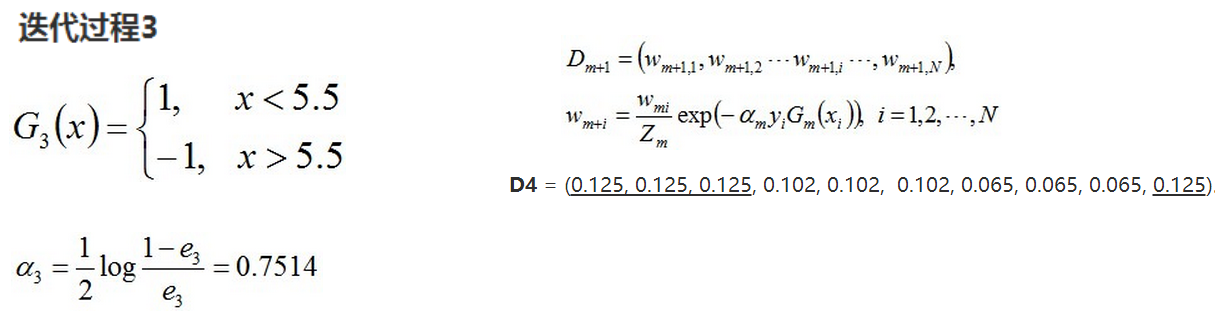
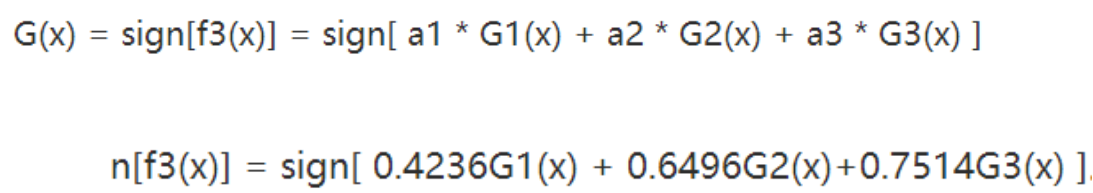
【机器学习】--Adaboost从初始到应用的更多相关文章
- 机器学习——AdaBoost元算法
当做重要决定时,我们可能会考虑吸取多个专家而不只是一个人的意见.机器学习处理问题也是这样,这就是元算法(meta-algorithm)背后的思路. 元算法是对其他算法进行组合的一种方式,其中最流行的一 ...
- 机器学习——Adaboost
1 Adaboost 的提出 1990年,Schapire最先构造出一种多项式级的算法,即最初的Boost算法; 1993年,Drunker和Schapire第一次将神经网络作为弱学习器,应用Boos ...
- [机器学习]-Adaboost提升算法从原理到实践
1.基本思想: 综合某些专家的判断,往往要比一个专家单独的判断要好.在”强可学习”和”弱可学习”的概念上来说就是我们通过对多个弱可学习的算法进行”组合提升或者说是强化”得到一个性能赶超强可学习算法的算 ...
- 【机器学习】--LDA初始和应用
一.前述 LDA是一种 非监督机器学习 技术,可以用来识别大规模文档集(document collection)或语料库(corpus)中潜藏的主题信息.它采用了词袋(bag of words)的方法 ...
- 【机器学习】--xgboost初始之代码实现分类
一.前述 上节我们讲解了xgboost的基本知识,本节我们通过实例进一步讲解. 二.具体 1.安装 默认可以通过pip安装,若是安装不上可以通过https://www.lfd.uci.edu/~goh ...
- Rapid Object Detection using a Boosted Cascade of Simple Features 部分翻译
Rapid ObjectDetection using a Boosted Cascade of Simple Features 使用简单特征级联分类器的快速目标检测 注:部分翻译不准处以红色字体给出 ...
- 【机器学习笔记之四】Adaboost 算法
本文结构: 什么是集成学习? 为什么集成的效果就会好于单个学习器? 如何生成个体学习器? 什么是 Boosting? Adaboost 算法? 什么是集成学习 集成学习就是将多个弱的学习器结合起来组成 ...
- 机器学习之Adaboost (自适应增强)算法
注:本篇博文是根据其他优秀博文编写的,我只是对其改变了知识的排序,另外代码是<机器学习实战>中的.转载请标明出处及参考资料. 1 Adaboost 算法实现过程 1.1 什么是 Adabo ...
- 机器学习之AdaBoost原理与代码实现
AdaBoost原理与代码实现 本文系作者原创,转载请注明出处: https://www.cnblogs.com/further-further-further/p/9642899.html 基本思路 ...
随机推荐
- Android监测手指上下左右滑动屏幕
在开发android程序时,有时会需要监测手指滑动屏幕,当手指朝上下左右不同方向滑动时做出不同的响应,那怎么去实现呢? 利用Android提供的手势监测器就可以很方便的实现,直接上代码(已测试通过) ...
- Python操作Redis之设置key的过期时间
对于一个已经存在的key,我们可以设置其过期时间,到了那个时间后,当你再去访问时,key就不存在了 有两种方式可以设置过期时间,一种是指定key从当前时间开始算起还能存活多久,时间单位有两个,一个是秒 ...
- bzoj 1485 [HNOI2009]有趣的数列 卡特兰数
把排好序的序列看成一对对括号,要把他们往原数列里塞,所以就是括号序合法方案数 即为卡特兰数 f(n)=Cn2nn+1 求的时候为避免除法,可以O(n)计算每个素数出现次数,最后乘起来,打完之后发现其实 ...
- 我的mfc基础知识点
最近由于作业的缘故,结交了mfc这个新朋友,虽然他对我还很是陌生,相信日久定能生情!现在记录一些学习的笔记,备忘. MFC提供了不同类型的设备描述表的类(绘图类):CDC.CPaintDC.CClie ...
- 浅谈surging服务引擎中的rabbitmq组件和容器化部署
1.前言 上个星期完成了surging 的0.9.0.1 更新工作,此版本通过nuget下载引擎组件,下载后,无需通过代码build集成,引擎会通过Sidecar模式自动扫描装配异构组件来构建服务引擎 ...
- 你真的了解String吗?(修正版)
修正前:new出来的对象,会在堆中存放真正的值: 大错特错!!!! 修正后:new出来的对象,堆存放的并不是真正的值,而是常量池中字符串常量的地址. 一.抛砖引玉 不知道大家在做面试题时是否会遇到 ...
- appium-desktop录制脚本二次开发,生成我司自动化脚本
目的 通过对appium-desktop脚本录制功能进行二次开发,使录制的java脚本符合我司自动化框架要求. 实现步骤 1.增加元素名称的输入框 由于ATK(我司自动化测试框架)脚本中元素是以“ap ...
- 『审慎』.Net4.6 Task 异步函数 比 同步函数 慢5倍 踩坑经历
异步Task简单介绍 本标题有点 哗众取宠,各位都别介意(不排除个人技术能力问题) —— 接下来:我将会用一个小Demo 把 本文思想阐述清楚. .Net 4.0 就有了 Task 函数 —— 异步编 ...
- [译] PEP 255--简单的生成器
我正打算写写 Python 的生成器,然而查资料时发现,引入生成器的 PEP 没人翻译过,因此就花了点时间翻译出来.如果在阅读时,你有读不懂的地方,不用怀疑,极有可能是我译得不到位.若出现这种情况,我 ...
- Spring Boot Web 自定义注解篇(注解很简单很好用)
自从spring 4.0 开放以后,可以添加很多新特性的注解了.使用系统定义好的注解可以大大方便的提高开发的效率. 下面我贴一段代码来讲解注解: 通过小小的注解我们支持了以下功能: 使 spring. ...
