HDU p1294 Rooted Trees Problem 解题报告

http://www.cnblogs.com/keam37/p/3639294.html keam所有 转载请注明出处

Problem Description

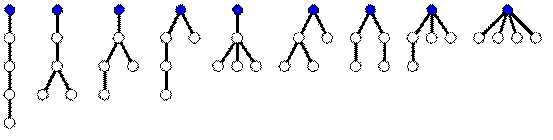
Give you two definitions tree and rooted tree. An undirected connected graph without cycles is called a tree. A tree is called rooted if it has a distinguished vertex r called the root. Your task is to make a program to calculate the number of rooted trees with n vertices denoted as Tn. The case n=5 is shown in Fig. 1.

Input

There are multiple cases in this problem and ended by the EOF. In each case, there is only one integer means n(1<=n<=40) .

Output

For each test case, there is only one integer means Tn.

Sample Input

1 2 5

Sample Output

1 1 9

分析：

题目比较容易读懂，就是求n个节点的树有多少种。

按照递推的思路，f[n]=f[a₁]*f[a₂]*….f[a_i];          其中 a₁+a₂+…+a_i=n 且a₁<=a₂<=….<=a_i

很自然想到这是整数拆分的样式

进一步考虑，对于n=a*sum[a]+b*sum[b]+c*sum[c]； sum[k]为一个拆分中k的个数

仅对sum[a]个 a计算

一个数a有f[a]种不同的拆分方式

就相当于从(f[a]个不同a)中选取sum[a]个(可以重复) 的排列

即 多重排列 C(f[a]+sum[a]-1,sum[a]);

再依次计算b,c累加即可.

参考代码

#include<iostream>
#define int64 __int64
using namespace std;

int64 f[41];
int cnt[41] , n;
//计算组合数
int64 C(int64 n,int64 m){
         m=m<(n-m)?m:(n-m);
         int64 ans=1;
         for(int i=1;i<=m;i++)
               ans=ans*(n-i+1)/i;
         return ans;
}
//拆分数并计算f[n]
int dfs(int temp, int left){
         if( left == 0 ){
               int64 ans = 1;
               for(int i = 1; i<=n ;i ++){
                     if(cnt[i] == 0)   continue;
                     //计算并累加多重排列
                     ans = ans * C(f[i] + cnt[i] - 1 , cnt[i]);
               }
               f[n] += ans;
               return 0;
         }
         for(int i=temp;i<=left;i++){
               cnt[i]++;   dfs(i,left-i);
               cnt[i]--;
         }
         return 0;
}
int main() {
         f[1] = f[2] = 1;
         for(n = 3; n <= 40 ; n++)    dfs(1,n-1);
         while(cin>>n)  cout<<f[n]<<endl;
         return 0;
}