正则化--L2正则化

请查看以下泛化曲线，该曲线显示的是训练集和验证集相对于训练迭代次数的损失。

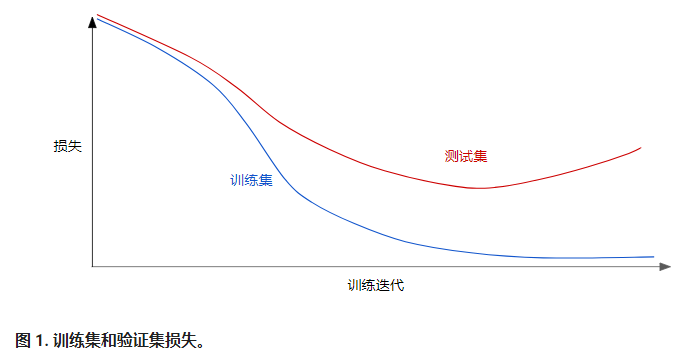
图 1 显示的是某个模型的训练损失逐渐减少，但验证损失最终增加。换言之，该泛化曲线显示该模型与训练集中的数据过拟合。根据奥卡姆剃刀定律，或许我们可以通过降低复杂模型的复杂度来防止过拟合，这种原则称为正则化。

也就是说，并非只是以最小化损失（经验风险最小化）为目标：

$$\text{minimize(Loss(Data|Model))}$$

而是以最小化损失和复杂度为目标，这称为结构风险最小化：

$$\text{minimize(Loss(Data|Model) + complexity(Model))}$$

现在，我们的训练优化算法是一个由两项内容组成的函数：一个是损失项，用于衡量模型与数据的拟合度，另一个是正则化项，用于衡量模型复杂度。

机器学习速成课程重点介绍了两种衡量模型复杂度的常见方式（这两种方式有些相关）：

• 将模型复杂度作为模型中所有特征的权重的函数。
• 将模型复杂度作为具有非零权重的特征总数的函数。

如果模型复杂度是权重的函数，则特征权重的绝对值越高，模型就越复杂。

我们可以使用 L2 正则化公式来量化复杂度，该公式将正则化项定义为所有特征权重的平方和：

$$L_2 \text{regularization term} = || w||_2^2 = {w_1^2 + w_2^2 + w_n^2}$$

在这个公式中，接近于 0 的权重对模型复杂度几乎没有影响，而离群值权重则可能会产生巨大的影响。

$$\{w_1 = 0.2, w_2 = 0.5, w_3 = 5, w_4 = 1, w_5 = 0.25, w_6 = 0.75\}$$

L2 正则化项为 26.915：

\[w_1^2 + w_2^2 + {w_3^2} + w_4^2 + w_5^2 + w_6^2\]

\[= 0.2^2 + 0.5^2 + {5^2} + 1^2 + 0.25^2 + 0.75^2\]

\[= 0.04 + 0.25 + {25} + 1 + 0.0625 + 0.5625\]

\[= 26.915\]
```

但是w3的平方值为25，几乎贡献了全部的复杂度。所有 5 个其他权重的平方和对 L2 正则化项的贡献仅为 1.915。

---

引用

简化正则化 (Regularization for Simplicity)：L₂ 正则化