MicroNet: 低秩近似分解卷积以及超强激活函数，碾压MobileNet | 2020新文分析

论文提出应对极低计算量场景的轻量级网络MicroNet，包含两个核心思路Micro-Factorized convolution和Dynamic Shift-Max，Micro-Factorized convolution通过低秩近似将原卷积分解成多个小卷积，保持输入输出的连接性并降低连接数，Dynamic Shift-Max通过动态的组间特征融合增加节点的连接以及提升非线性，弥补网络深度减少带来的性能降低。从实验结果来看，MicroNet的性能十分强劲

 

来源：晓飞的算法工程笔记 公众号

论文: MicroNet: Towards Image Recognition with Extremely Low FLOPs

• 论文地址：https://arxiv.org/abs/2011.12289

Introduction

---

  论文将研究定义在一个资源十分紧张的场景：在6MFLOPs的限定下进行分辨率为224x224的1000类图片分类。对于MobileNetV3，原版的计算量为112M MAdds，将其降低至12M MAdds时，top-1准确率从71.7%降低到了49.8%。可想而知，6M MAdds的场景是十分苛刻的，需要对网络进行细心的设计。常规的做法可直接通过降低网络的宽度和深度来降低计算量，但这会带来严重的性能下降。

  为此，论文在设计MicroNet时主要遵循两个设计要领：1）通过降低特征节点间的连通性来避免网络宽度的减少。2）通过增强非线性能力来补偿网络深度的减少。MicroNet分别提出了Micro-Factorized Convolution和Dynamic Shift-Max来满足上述两个原则，Micro-Factorized Convolution通过低秩近似减少输入输出的连接数但不改变连通性，而Dynamic Shift-Max则是更强有力的激活方法。从实验结果来看，仅需要6M MAdds就可以达到53.0%准确率，比12M MAdds的MobileNetV3还要高。

Micro-Factorized Convolution

---

  Micro-Factorized Convolution主要是对MobileNet的深度分离卷积进行更轻量化的改造，对pointwise convolution和depthwise convolution进行低秩近似。

Micro-Factorized Pointwise Convolution

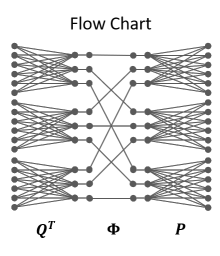
  论文将pointwise convoluton分解成了多个稀疏的卷积，如上图所示，先对输入进行维度压缩，shuffle后进行维度扩展，个人感觉这部分与shufflenet基本一样。这样的操作在保证输入与输出均有关联的情况下，使得输入与输出之间的连接数减少了很多。

  假定卷积核\(W\)的输入输出维度相同，均为\(C\)，Micro-Factorized Convolution可公式化为：

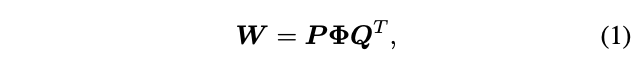
  \(W\)为\(C\times C\)矩阵，\(Q\)为\(C\times \frac{C}{R}\)矩阵，用于压缩输入，\(P\)为\(C\times \frac{C}{R}\)矩阵，用于扩展输出，\(Q\)和\(P\)均为包含\(G\)个块的对角矩阵。\(\Phi\)为\(\frac{C}{R}\times \frac{C}{R}\)排列矩阵，功能与shufflenet的shuffle channels操作一样。分解后的计算复杂度为\(\mathcal{O}=\frac{2C^2}{RG}\)，上图展示的参数为\(C=18\),\(R=2\),\(G=3\)。\(G\)的大小由维度\(C\)和下降比例\(R\)而定：

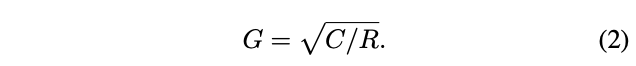
  公式2是由维度数\(C\)与每个输出维度对应输入维度的连接数\(E\)之间的关系推导所得，每个输出维度与\(\frac{C}{RG}\)个中间维度连接，每个中间维度与\(\frac{C}{G}\)个输入维度连接，因此\(E=\frac{C^2}{RG^2}\)。假如固定计算复杂度\(\mathcal{O}=\frac{2C^2}{RG}\)和压缩比例R，得到：

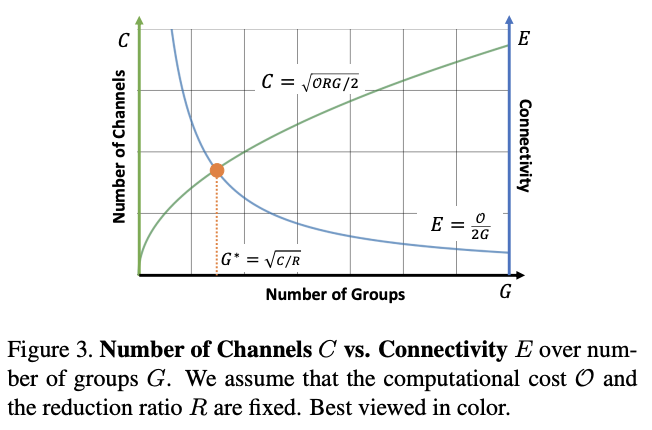
  公式3的可视化如图3所示，随着\(G\)和\(C\)的增加，\(E\)在减少。在两者的交点\(G=\sqrt{C/R}\)处，每个输出维度刚好只与每个输入维度连接了一次，其中\(\Phi\)的shuffle作用很大。从数学上来说，矩阵\(W\)可分为\(G\times G\)个秩为1的小矩阵，从小节开头处的分解示意图可看出，矩阵\(W\)中\((i,j)\)小矩阵实际为\(P\)矩阵的\(j\)列与\(Q^T\)的\(j\)行的矩阵相乘结果(去掉空格)。

Micro-Factorized Depthwise Convolution

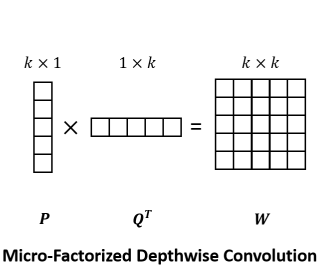
  论文将\(k\times k\)深度卷积分解为\(k\times 1\)卷积与\(1\times k\)卷积，计算与公式1类似，\(\Phi\)为标量1，如上图所示，可将计算复杂度从\(\mathcal{O}(k^2C)\)降低为\(\mathcal{O}(kC)\)。

Combining Micro-Factorized Pointwise and Depthwise Convolutions

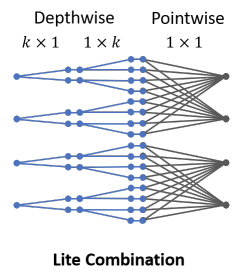
  论文提供了两种Micro-Factorized Pointwise Convolution和Micro-Factorized Depthwise Convolution的组合方法：

• 常规组合，直接将两种操作进行组合，这种情况下，两种操作的输入输出维度都是\(C\)。
• lite组合，如上图所示，增加Micro-Factorized Depthwise Convolution的卷积核数，对输入进行维度扩展，然后用Micro-Factorized Pointwise Convolution进行维度压缩。

  相对于常规组合，lite组合的计算更高效，由于减少了Pointwise卷积的计算量，足以弥补depthwise卷积核的增加。

Dynamic Shift-Max

---

  论文提出Dynamic Shift-Max融合输入特征，综合输出维度对应的各分组的特征(循环偏移)进行非线性输出。由于Micro-Factorized pointwise convolution仅关注分组内的连接，Dynamic Shift-Max可作为其补充。

Definition

  定义\(C\)维输入向量\(x=\{x_i\}(i=1,\cdots, C)\)，将输入分为\(G\)组，每组包含\(\frac{C}{G}\)维，\(N\)维向量的循环偏移可表示为\(x_N(i)=x_{(i+N)} mod\ C\)，将维度循环偏移扩展到分组循环偏移：

  \(x_{\frac{C}{G}}(i,j)\)对应第\(i\)维输入\(x_i\)关于\(j\)分组的偏移， Dynamic Shift-Max将多个(\(J\))分组偏移进行结合：

  \(a^k_{i,j}(x)\)为输入相关的参数，可由平均池化接两个全连接层简单实现。对于输出\(y_i\)，将对应每个分组的偏移维度进行\(K\)次融合，每次融合都有专属的\(a^k_{i,j}(x)\)参数，最后取融合结果的最大值。

Non-linearity

  Dynamic Shift-Max提供了两方面的非线性：

• 输出\(K\)个的融合\(J\)个分组维度的结果中的最大值，类似于考虑多种目标特征
• 参数\(a^k_{i,j}(x)\)是输入相关的函数，这是动态的

  上述两个特性使得Dynamic Shift-Max表达能力更强，能够弥补网络深度减少带来的损失。最近提出的dynamic ReLU可认为是Dynamic Shift-Max的\(J=1\)特例，仅考虑每个维度自身。

Connectivity

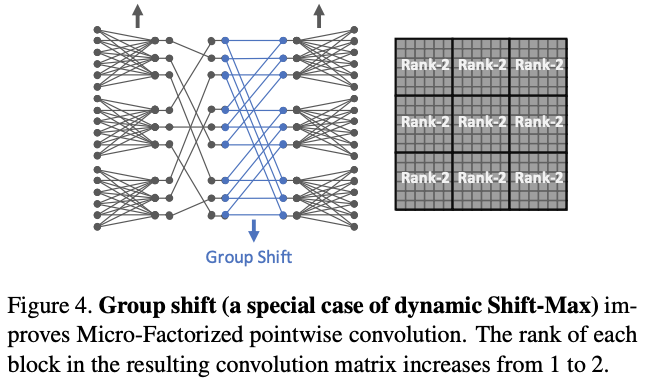
  Dynamic Shift-Max能够提升组间的维度交流，弥补MicroFactorized pointwise convolution只专注于组内连接的不足。图4为简单的静态分组偏移\(y_i=a_{i,0}x_{\frac{C}{G}}(i,0)+a_{i,1}x_{\frac{C}{G}}(i,1)\)，\(K=1\)，\(J=2\)以及固定的\(a^k_{i,j}\)，注意排列矩阵\(\Phi\)与前面的不太一样。可以看到，尽管这样的设计很简单，但依然能够有效地提升输入输出的关联性(矩阵\(W\)的秩也从1升为2)。

Computational Complexity

  Dynamic Shift-Max包含\(CJK\)个参数\(a^k_{i,j}\)，计算复杂度包含3部分：

• 平均池化(后面的两个全连接输出输出为1，可忽略)：\(\mathcal{O}(HWC)\)
• 生成公式5的参数\(a^k_{i,j}(x)\)：\(\mathcal{O}(C^2JK)\)
• 对每个维度和特征图位置进行Dynamic Shift-Max: \(\mathcal{O}(HWCJK)\)

  当\(J\)和\(K\)很小时，整体的计算量会很轻量，论文设置为\(J=2\)以及\(K=2\)。

MicroNet Architecture

---

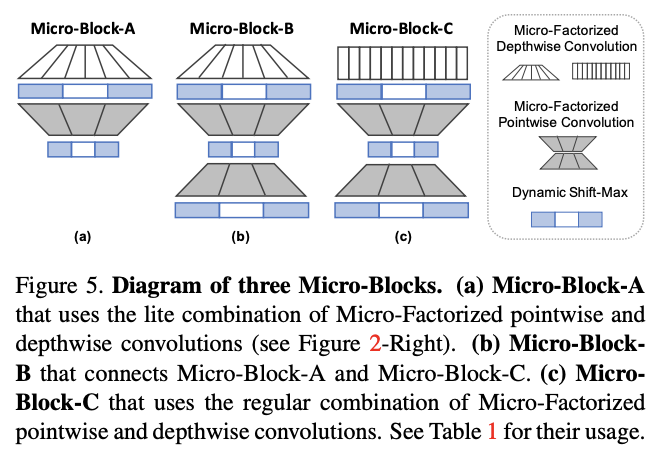
  论文设计了3种不同的Mircro-Block，里面均包含了Dynamic Shift-Max作为激活函数：

• Micro-Block-A：使用lite组合，对分辨率较高的低维特征特别有效。
• Micro-Block-B：在Micro-Block-A基础上加了一个 MicroFactorized pointwise convolution进行维度扩展，每个MicroNet仅包含一个Micro-Block-B。
• Micro-Block-C：与Micro-Block-B类似，将lite组合替换为常规组合，能够集中更多的计算在维度融合，如果输入输出维度一样，则增加旁路连接。

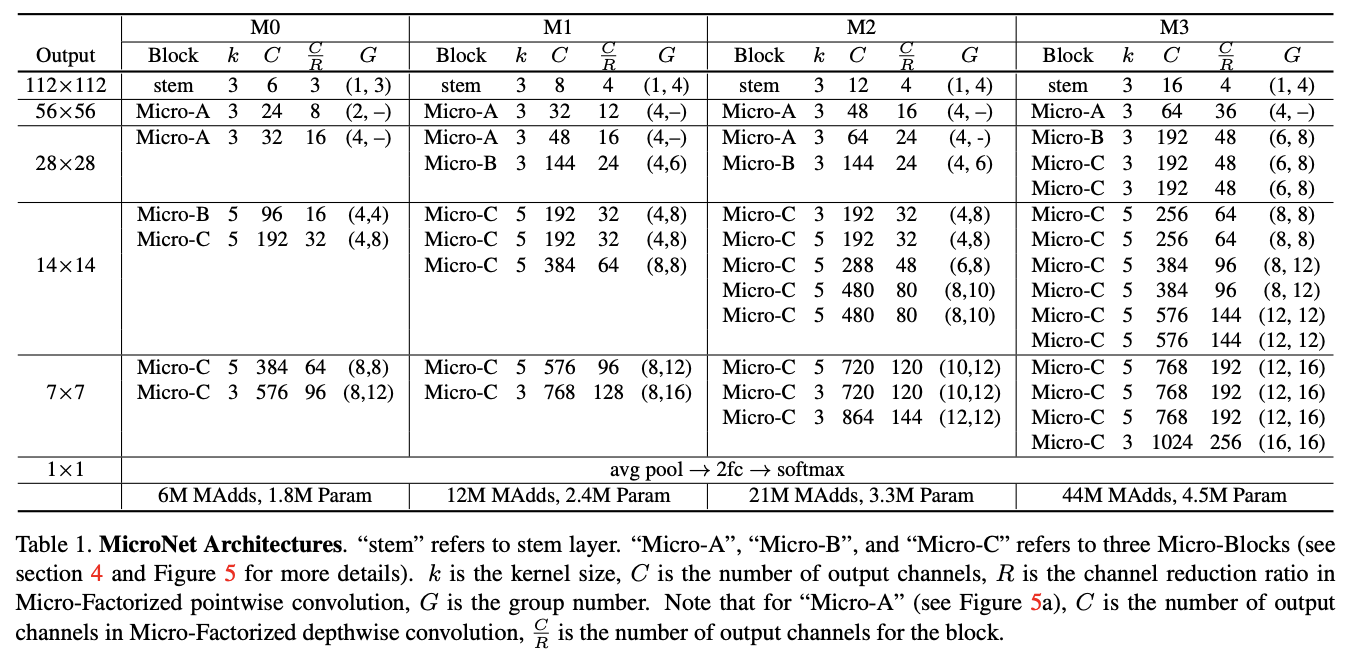
  MicroNet的结构如表1所示，需要注意的是两种卷积的分组数\(G_1\)和\(G_2\)，论文将公式2的约束改为\(G_1G_2=C/R\)。

Experiments: ImageNet Classification

---

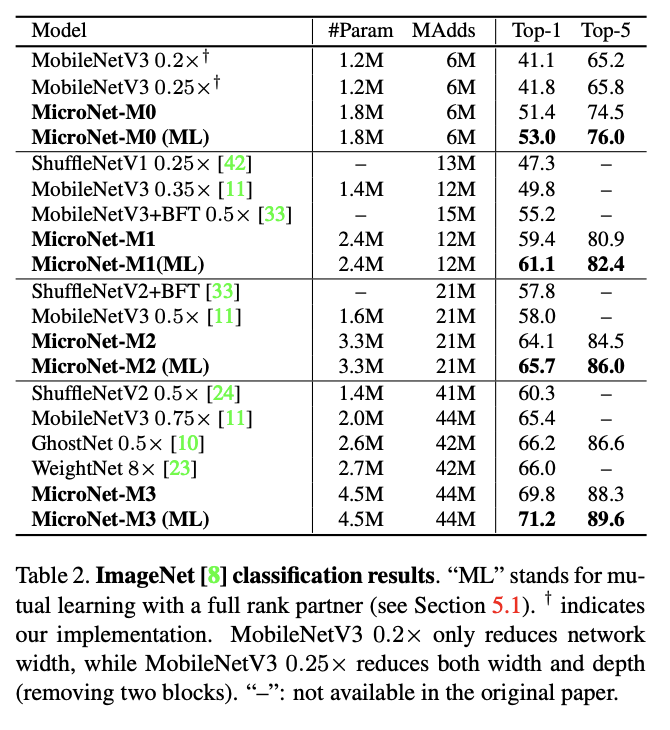
  ImageNet上的结果。

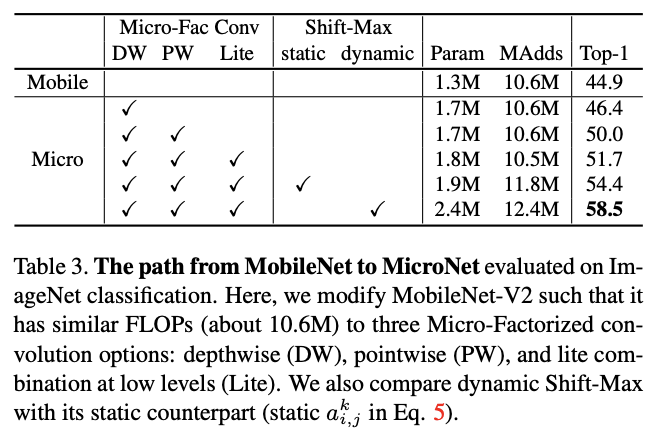
  从MobileNet到MicroNet的修改对比，每个修改的提升都很大，论文还有很多关于各模块的超参数对比实验，由兴趣的可以去看看。

Conclusion

---

  论文提出应对极低计算量场景的轻量级网络MicroNet，包含两个核心思路Micro-Factorized convolution和Dynamic Shift-Max，Micro-Factorized convolution通过低秩近似将原卷积分解成多个小卷积，保持输入输出的连接性并降低连接数，Dynamic Shift-Max通过动态的组间特征融合增加节点的连接以及提升非线性，弥补网络深度减少带来的性能降低。从实验结果来看，MicroNet的性能十分强劲。

 

 

 

如果本文对你有帮助，麻烦点个赞或在看呗～

更多内容请关注 微信公众号【晓飞的算法工程笔记】