PID控制器开发笔记之七：微分先行PID控制器的实现

　　前面已经实现了各种的PID算法，然而在某些给定值频繁且大幅变化的场合，微分项常常会引起系统的振荡。为了适应这种给定值频繁变化的场合，人们设计了微分先行算法。

1、微分先行算法的思想

　　微分先行PID控制是只对输出量进行微分，而对给定指令不起微分作用，因此它适合于给定指令频繁升降的场合，可以避免指令的改变导致超调过大。微分先行的基本结构图：

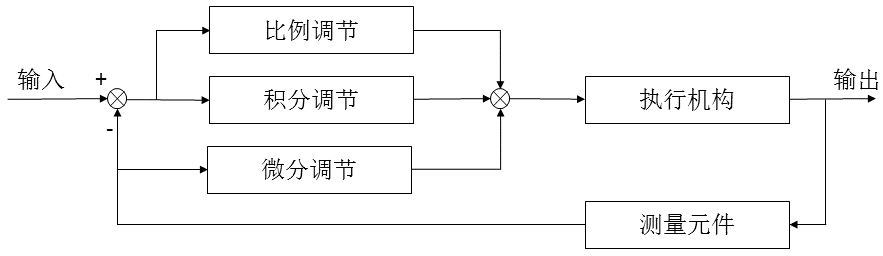
　　根据上面的结构图，我们可以推出PID控制器的输出公式，比例和积分是不变的只是微分部分变为只对对象输出积分，记为y，我们对微分部分引入一阶惯性滤波：，可记微分部分的传递函数如下：

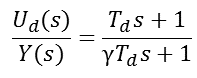
　　于是微分部分可以推导出如下的公式：

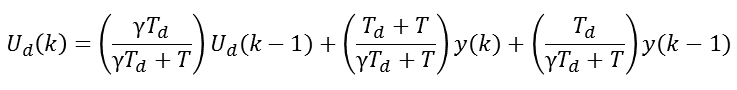
　　前面我们在推导PID的公式时曾规定：Kd=Kp*Td/T，于是我们将其带入公式可得：

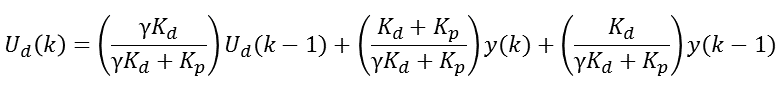
　　于是我们就可以得到微分先行的离散化公式：

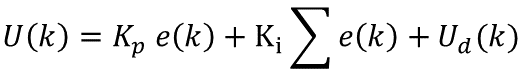
　　这即是位置型PID的计算公式了，我们也可以使用前面的方法推导增量型的计算公式如下：

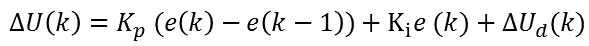
　　从上面的公式我们发现，微分部分只与测量值有关，而且与连续的几个测量值都有关。而与设定值没有关系，设定值的阶跃变化不会造成高频的干扰。

2、算法实现

　　前面我们已经简单的介绍了微分现行的基本结构，也推导了位置型以及增量型公式，接下来我们根据前面对其基本思想的描述，来实现基于微分先行的PID算法实现，同样是包括位置型和增量型两种实现方式。

（1）位置型PID算法实现

　　关于微分先行PID算法的公式我们已经推导出来了，编码实现就是在公式的基础上将其计算机语言化。同样的，首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float result;     //输出值

   float integral;   //积分值

   float derivative;      //微分项

   float lastPv;     //前一拍的测量值

   float gama;      //微分先行滤波系数

 }PID;

　　接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

 float c1,c2,c3,temp;

   thisError=vPID->setpoint-processValue;

   vPID->integral+=thisError;

   temp= vPID-> gama * vPID-> derivativegain + vPID-> proportiongain;

   c3= vPID-> derivativegain/temp;

   c2=( vPID-> derivativegain+ vPID-> proportiongain)/temp;

   c1= vPID-> gama*c3;

 vPID-> derivative=c1* vPID-> derivative+c2* processValue+c3* vPID-> lastPv;

 vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID-> derivative;

   vPID->lasterror=thisError;

 vPID-> lastPv= processValue;

 }

　　对于微分先行的位置型PID控制器来说，本次的微分项不仅与上一拍的微分结果有关，而且与上一拍的测量值有关。

（2）增量型PID算法实现

　　微分先行增量型PID控制算法的实现就是以前面的增量型公式为基础。微分先行的比例与积分部分并没有什么变化，当然积分部分也可以采用各种优化算法。而微分部分以增量型公式实现即可，首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float preerror;     //前两拍偏差

   float deadband;     //死区

   float result;      //输出值

   float deltadiff;              /*微分增量*/

   float integralValue;          /*积分累计量*/

   float gama;                   /*微分先行滤波系数*/

   float lastPv;                 /*上一拍的过程测量值*/

   float lastDeltaPv;            /*上一拍的过程测量值增量*/

 }PID;

　　接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

   float increment;

   float pError,iError;

 float c1,c2,c3,temp;

 float deltaPv;

   temp= vPID-> gama * vPID-> derivativegain + vPID-> proportiongain;

   c3= vPID-> derivativegain/temp;

   c2=( vPID-> derivativegain+ vPID-> proportiongain)/temp;

   c1= vPID-> gama*c3;

   deltaPv= processValue- vPID-> lastDeltaPv

 vPID-> deltadiff =c1* vPID-> deltadiff +c2* deltaPv +c3* vPID-> lastDeltaPv;

   thisError=vPID->setpoint-processValue; //得到偏差值

   pError=thisError-vPID->lasterror;

   iError=thisError;

   increment=vPID->proportiongain*pError+vPID->integralgain*iError+ vPID-> deltadiff;   //增量计算

   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算

 vPID->lastDeltaPv=deltaPv;

   vPID->lastPv= processValue;

   vPID->lasterror=thisError;

   vPID->result+=increment;

 }

　　这就实现了一个最简单的微分先行的增量型PID控制器，与一般的PID控制器相比，还需要知道前一拍的测量值、前一拍的测量值增值以及前一拍的微分增量，其余的只需要按公式完成即可。

3、总结

　　微分先行由于微分部分只对测量值起作用所以可以消除设定值突变的影响，还可以引入低通滤波，甚至在必要时将比例作用也可进行相应的改进。其实用于设定值会频繁改变的过程对象，防止设定值的频繁波动造成系统的不稳定。该控制对于改善系统的动态特性是有好处的，但势必影响响应的速度，需全面考虑。

欢迎关注：