BZOJ 1731: [Usaco2005 dec]Layout 排队布局

Description

Like everyone else, cows like to stand close to their friends when queuing for feed. FJ has N (2 <= N <= 1,000) cows numbered 1..N standing along a straight line waiting for feed. The cows are standing in the same order as they are numbered, and since they can be rather pushy, it is possible that two or more cows can line up at exactly the same location (that is, if we think of each cow as being located at some coordinate on a number line, then it is possible for two or more cows to share the same coordinate). Some cows like each other and want to be within a certain distance of each other in line. Some really dislike each other and want to be separated by at least a certain distance. A list of ML (1 <= ML <= 10,000) constraints describes which cows like each other and the maximum distance by which they may be separated; a subsequent list of MD constraints (1 <= MD <= 10,000) tells which cows dislike each other and the minimum distance by which they must be separated. Your job is to compute, if possible, the maximum possible distance between cow 1 and cow N that satisfies the distance constraints.

当排队等候喂食时，奶牛喜欢和它们的朋友站得靠近些。FJ有N（2<=N<=1000）头奶牛，编号从1到N，沿一条直线站着等候喂食。奶牛排在队伍中的顺序和它们的编号是相同的。因为奶牛相当苗条，所以可能有两头或者更多奶牛站在同一位置上。即使说，如果我们想象奶牛是站在一条数轴上的话，允许有两头或更多奶牛拥有相同的横坐标。一些奶牛相互间存有好感，它们希望两者之间的距离不超过一个给定的数L。另一方面，一些奶牛相互间非常反感，它们希望两者间的距离不小于一个给定的数D。给出ML条关于两头奶牛间有好感的描述，再给出MD条关于两头奶牛间存有反感的描述。（1<=ML,MD<=10000，1<=L,D<=1000000）你的工作是：如果不存在满足要求的方案，输出-1；如果1号奶牛和N号奶牛间的距离可以任意大，输出-2；否则，计算出在满足所有要求的情况下，1号奶牛和N号奶牛间可能的最大距离。

Input

* Line 1: Three space-separated integers: N, ML, and MD. * Lines 2..ML+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at most D (1 <= D <= 1,000,000) apart. * Lines ML+2..ML+MD+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at least D (1 <= D <= 1,000,000) apart.

Output

* Line 1: A single integer. If no line-up is possible, output -1. If cows 1 and N can be arbitrarily far apart, output -2. Otherwise output the greatest possible distance between cows 1 and N.

Sample Input

4 2 1
1 3 10
2 4 20
2 3 3

INPUT DETAILS:

There are 4 cows. Cows #1 and #3 must be no more than 10 units
apart, cows #2 and #4 must be no more than 20 units apart, and cows
#2 and #3 dislike each other and must be no fewer than 3 units apart.

Sample Output

四只牛分别在0，7，10，27.

Solution:

　　本题依然是差分约束。。。

　　注意是求最大距离，所以尽可能用大的更新小的距离。

　　我们分别罗列一下约束条件（以下出现的$s[x]$表示第$x$头牛的距离）：

　　　　1、$s[v]-s[u]\leq c$即$s[u]+c\geq s[v]$，建边$w[u,v]=c$（表示$v$比$u$大$c$）

　　　　2、$s[v]-s[u]\geq c$即$s[v]-c\geq s[u]$，建边$w[v,u]=-c$（表示$u$比$v$小$c$）

　　　　3、因为牛按顺序排列，所以还需满足$s[u]\leq s[u+1]$，建边$w[u+1,u]=0$（用大的更新小的，尽可能使小的等于大的距离）

　　然后，我们应该求的是最短路，很容易理解，因为求最小值时是跑最长路，现在就是求最短路嘛！（什么鬼？其实很简单）

　　看图（盗的）：

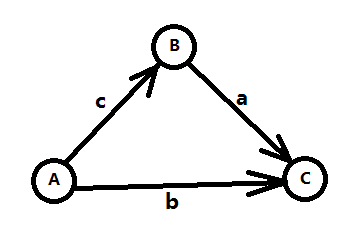
　　　图中表示的约束条件为:$(1)\;s[B]-s[A]\leq c,\;\;(2)\;s[C]-s[B]\leq a,\;\;(3)\;s[C]-s[A]\leq b$，我们现在要求$(s[C]-s[A])_{max}$，那么很显然将不等式组中的$(1)+(2)$便能得到$s[C]-s[A]\leq a+c$，由于受到两个约束那么最后$s[C]-s[A]$的答案就是$min(b,a+c)$，所以很显然是求最短路（至于求解最小值，只要将各式表示为$X\geq Y$的情况，建边，显然求最长路）。

　　那么我们搞清楚建图后，当出现环时输出$-1$，当出现$dis[n]$没有被更新时输出$-2$，否则就有解输出$dis[n]$。

代码：

#include<iostream>

#include<queue>

#include<cstdio>

#include<cstring>

#define il inline

using namespace std;

const int N=,inf=;

int n,m,k,to[N],net[N],w[N],dis[N],cnt,h[N],tot[N];

bool vis[N];

queue<int>q;

il int gi(){

    int a=;char x=getchar();

    while(x<''||x>'')x=getchar();

    while(x>=''&&x<='')a=(a<<)+(a<<)+x-,x=getchar();

    return a;

}

il void add(int u,int v,int c){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt,w[cnt]=c;}

int main(){

    n=gi(),m=gi(),k=gi();

    int u,v,c;

    while(m--){

        u=gi(),v=gi(),c=gi();

        add(u,v,c);

    }

    while(k--){

        u=gi(),v=gi(),c=gi();

        add(v,u,-c);

    }

    memset(dis,0x3f,sizeof(dis));

    dis[]=;q.push();

    while(!q.empty()){

        int u=q.front();q.pop();vis[u]=;tot[u]++;

        if(tot[u]==n){cout<<-;return ;}

        for(int i=h[u];i;i=net[i])

            if(dis[to[i]]>dis[u]+w[i]){

                dis[to[i]]=dis[u]+w[i];

                if(!vis[to[i]])q.push(to[i]),vis[to[i]]=;

            }

    }

    if(dis[n]>=inf)cout<<-;

    else cout<<dis[n];

    return ;

}