Luogu 4363 [九省联考2018]一双木棋chess

发现数据范围很小，想到状压dp，然后就愣住不会了。

表示太菜了并没有接触过轮廓线dp这种操作。

首先发现合法的操作过程中一定是这样子的：

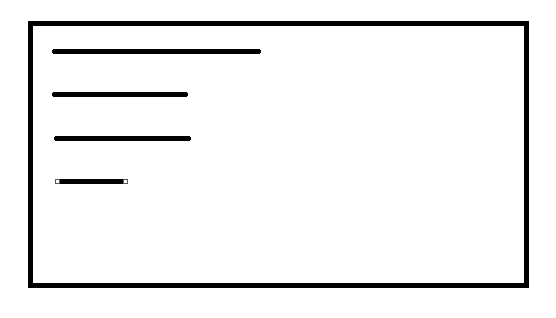
按照行来看发现每一行单调不递增。

我们用$1$来表示竖着的轮廓线，用$0$来表示横着的轮廓线，那么来看一下样例，一个棋子都没有放的状态是$00011$，而在唯一的$(1, 1)$位置放上第一个棋子之后状态就变成了$00101$。

其实是这么画出来的：

    

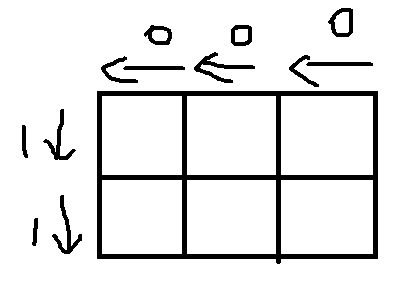
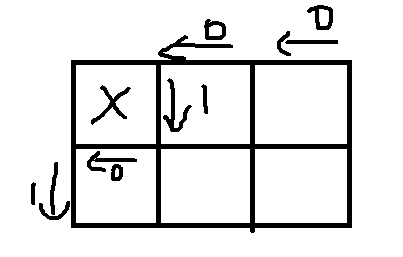
这样子就发现其实一个$1$后面有多少个$0$就代表放到了第几个，因为每一行是单调不递减的我们就可以从这个状态的表示中算出当前放到了哪里。

玩一下放旗子的过程发现，其实转移的过程就相当于找到一个左边是$0$的$1$，然后把两个数交换一下。

因为轮廓线的大小是肯定的，所以有效状态的个数就相当于从$(1, m)走到$(n, 1)$，并$在$n + m$步中选择$n$步向下走的方案数，为$\binom{n + m}{n}$个。

然而转移顺序似乎并不显然，记忆化搜索？

其实这个搜索还有一个高端的名字叫做对抗搜索，先手希望价值最大，后手希望价值最小，应该比较显然。

时间复杂度是$O(\binom{n + m}{n})$。

搜的时候注意先记$vis$再转移。

#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;

const int N = ;
const int S = ( << ()) + ;
const ll P = 1e9 + ;
const ll inf = (ll) << ;

int n, m;
ll a[N][N], b[N][N], f[S];
bool vis[S];

template <typename T>
inline void read(T &X) {
    X = ; char ch = ; T op = ;
    for(; ch > ''|| ch < ''; ch = getchar())
        if(ch == '-') op = -;
    for(; ch >= '' && ch <= ''; ch = getchar())
        X = (X << ) + (X << ) + ch - ;
    X *= op;
}

inline void chkMax(ll &x, ll y) {
    if(y > x) x = y;
}

inline void chkMin(ll &x, ll y) {
    if(y < x) x = y;
}

ll dfs(int s, int who) {
    if(vis[s]) return f[s];
    vis[s] = ;
    ll res = who ? -inf : inf;
    for(int i = , x = n + , y = ; i < n + m; i++) {
        if((s >> i) & ) x--;
        else y++;
        if(((s >> i) & ) !=  || i == n + m - ) continue;
        int to = s ^ ( << i);
        if(who) chkMax(res, dfs(to, who ^ ) + a[x][y]);
        else chkMin(res, dfs(to, who ^ ) - b[x][y]);
    }
    return f[s] = res;
}

int main() {
    read(n), read(m);
    for(int i = ; i <= n; i++)
        for(int j = ; j <= m; j++)
            read(a[i][j]);
    for(int i = ; i <= n; i++)
        for(int j = ; j <= m; j++)
            read(b[i][j]);

    f[(( << n) - ) << m] = , vis[(( << n) - ) << m] = ;
    printf("%lld\n", dfs(( << n) - , ));
    return ;
}