Canvas学习笔记——动画中摩擦力的运用

摩擦力是与物体运动方向相反的力。我们在处理物体运动时，常把物体分解水平(X轴)方向和竖直(Y轴)方向的运动(比如平抛运动)，但在处理摩擦力时，如果把摩擦力分解为X轴和Y轴上的阻力，就会出现某条轴上速度为0，而另一条轴还在运动的奇怪现象。为此，处理摩擦力时应将物体最终运动的方向作为基准。

首先计算出合速度：

var speed = Math.sqrt(vx * vx + vy * vy);

分析后可知

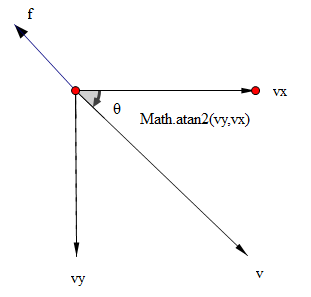
夹角θ可通过Math.atan2算出：

var angle = Math.atan2(vy,vx);

接下就是由速度减去摩擦力，但要注意不能速度变为负值，这样会改变物体的运动状态：

if(speed > friction) {
    speed -= friction;
} else {
    speed = 0;
}

在得到中和了摩擦力的速度以后，再将速度分解为水平和竖直方向的运动：

vx = Math.cos(angle) * speed;
vy = Math.sin(angle) * speed;

// > 16 & 0xff,
g = color >> 8 & 0xff,
b = color >> 0xff,
a = (alpha 1) ? 1 : alpha);

if(a === 1) {
return 'rgb('+r+','+g+','+b+')';
} else {
return 'rgba('+r+','+g+','+b+','+a+')';
}
};

window.utils.parseColor = function (color, toNumber) {
if (toNumber === true) {
if (typeof color === 'number') {
return (color | 0); //chop off decimal
}
if (typeof color === 'string' && color[0] === '#') {
color = color.slice(1);
}
return window.parseInt(color, 16);
} else {
if (typeof color === 'number') {
color = '#' + ('00000' + (color | 0).toString(16)).substr(-6); //pad
}
return color;
}
};

window.utils.containsPoint = function (rect, x, y) {
return !(x rect.x + rect.width ||
y rect.y + rect.height);
};

window.utils.intersects = function (rectA, rectB) {
return !(rectA.x + rectA.width 0) {
ctx.stroke();
}
ctx.restore();
};

function Ship () {
this.x = 0;
this.y = 0;
this.width = 25;
this.height = 20;
this.rotation = 0;
this.showFlame = false;
}

Ship.prototype.draw = function (ctx) {
ctx.save();
ctx.translate(this.x, this.y);
ctx.rotate(this.rotation);

ctx.lineWidth = 1;
ctx.strokeStyle = "#ffffff";
ctx.beginPath();
ctx.moveTo(10, 0);
ctx.lineTo(-10, 10);
ctx.lineTo(-5, 0);
ctx.lineTo(-10, -10);
//ctx.lineTo(10, 0);
ctx.closePath();
ctx.stroke();

if (this.showFlame) {
ctx.beginPath();
ctx.moveTo(-7.5, -5);
ctx.lineTo(-15, 0);
ctx.lineTo(-7.5, 5);
ctx.stroke();
}
ctx.restore();
};
// ]]>

 

// friction) {
speed -= friction;
} else {
speed = 0;
}

vx = Math.cos(angle) * speed;
vy = Math.sin(angle) * speed;

ball.x += vx;
ball.y += vy;
ball.draw(ctx);
})();
})();
// ]]>

虽然上面是计算摩擦力的正确方法，但太过繁琐了，还有一个简便方法

(function() {
            window.requestAnimFrame(arguments.callee,canvas);
            ctx.clearRect(0,0,canvas.width,canvas.height);

            vx *= 0.9;
            vy *= 0.9;

            ball.x += vx;
            ball.y += vy;
            ball.draw(ctx);
})();

就是将速度分量分别乘以一个摩擦力系数，这个方法的运动效果和之前没有差别，但这个方法永远不会停止，还需要做一些判断以减少运算量：

if(Math.abs(vx) > 0.001) {
    vx *= friction;
    ball.x += vx;
} 

在了解了如何计算摩擦力后，再来看看它的应用。

 

// right) {
ship.x = left - ship.width / 2;
} else if(ship.x + ship.width / 2 bottom) {
ship.y = top - ship.height / 2;
} else if(ship.y + ship.height / 2