【Nim游戏】高僧斗法

　　

　　先来看看Nim定理：

 //  若干堆硬币，二人轮流取，从一堆硬币中取几个  直到某个人不能取硬币  那这个人就输了
 //  3  4  5
 //  3  3    把硬币变成相同的  那么你就赢了  因为你可以跟着另一个人一样的取法
 //  尼姆定理：  无偏差的二人游戏  =====  尼姆堆
 /*
  *      11
  *     100
  *   ^ 101
  * ------------
  *     010
  *  先手：若非 0，必赢，因为可以把局面变成0这个局面
  *      若是 0，必输，因为这个局面本身就是赢的，你随便动一步，那另一个人保持跟你同步，所以最后必输。
  */
 public class Nim {

     public static void main(String[] args) {
         int []A = {3,3};
         boolean res = solve(A);
         System.out.println(res);
     }

     static boolean solve(int []A){
         int res = 0;
         for (int i = 0; i < A.length; i++) {
             res ^= A[i];
         }
         System.out.println(Integer.toBinaryString(res));
         return res !=0;
     }

 }

　　再来看这道题目：

　　

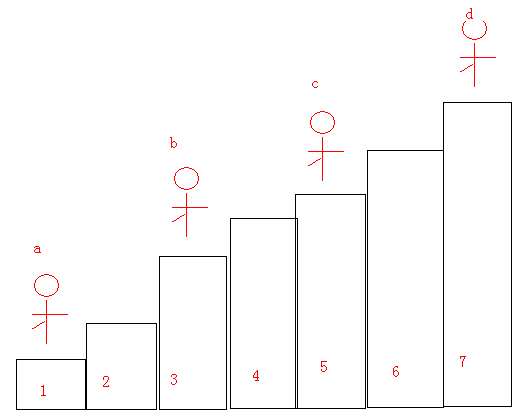
　　我们可以将和尚从后往前（从左到右）两两配对，若为奇数则在最高位补充一个假想的和尚，在同一对和尚中，如果对手移动前一个和尚，你总能移动后一个和尚相同的步数，所以一对和尚的前一个和尚与前面一对和尚的后一个和尚之间有多少台阶是没有影响的。所以只要考虑同一对和尚之间有多少台阶就行了，这样就转化为了Nim游戏。

　　如图： a与b配对， c与d配对 ，那么b与c之间的台阶是没有影响的，无论b怎么移动，a总能够移动相同的步数。如果该Nim游戏为必胜，那么我们只要移动配对和尚中的后一和尚就好了，如果对手想要破坏这种Nim游戏，即他想移动配对中的前一和尚，那么我们可以移动后面一对的前一个和尚使得依然保持Nim游戏的局势。如果Nim游戏必败，那么先手者可能想破坏Nim游戏，那么后手者按照刚才的方式保持Nim游戏即可。

　　代码：

 import java.util.Scanner;

 //   高僧斗法  所有这类的博弈问题都可以归结为尼姆游戏 Nim
 /*
  *   高僧斗法   =====>  尼姆游戏
  *   把小和尚位置间的空隙  === >  尼姆堆
  *   偶数：两两组合
  *   奇数：在最高阶补充一个假想的小和尚
  *
  */
 public class Test {

     public static void main(String[] args) {
         Scanner in = new Scanner(System.in);
         String A = in.nextLine();
         String[] arrayA = A.split(" ");
         int[] NimHeap = new int[arrayA.length - 1];
         for(int i = 1;i < arrayA.length;i++)
             // 两个和尚的间距作为尼姆堆
             NimHeap[i - 1] = Integer.valueOf(arrayA[i]) - Integer.valueOf(arrayA[i - 1]) - 1;
         int sum = 0;

         // i+2 就是为了用一个for实现n为奇和偶的两种情况，奇数时最后一个数不分到组中，偶数时需要将其分到组中。
         for(int i = 0;i < NimHeap.length;i = i + 2)
             sum ^= NimHeap[i];

         if(sum == 0)
             System.out.println("-1");
         else {
             for(int i = 0;i < arrayA.length - 1;i++) {
                 for(int j = 1;j + Integer.valueOf(arrayA[i]) < Integer.valueOf(arrayA[i + 1]);j++) {
                     NimHeap[i] -= j;
                     if(i != 0)
                         NimHeap[i - 1] += j;
                     sum = 0;
                     for(int k = 0;k < NimHeap.length;k = k + 2)
                         sum ^= NimHeap[k];
                     if(sum == 0) {
                         System.out.println(arrayA[i]+" "+(Integer.valueOf(arrayA[i])+j));
                         return;
                     }
                     NimHeap[i] += j;
                     if(i != 0)
                         NimHeap[i - 1] -= j;
                 }
             }
         }
     }
 }

　　结果：