P5057 [CQOI2006]简单题

题目描述

有一个 n 个元素的数组，每个元素初始均为 0。有 m 条指令，要么让其中一段连续序列数字反转——0 变 1，1 变 0（操作 1），要么询问某个元素的值（操作 2）。 例如当 n = 20 时，10 条指令如下：

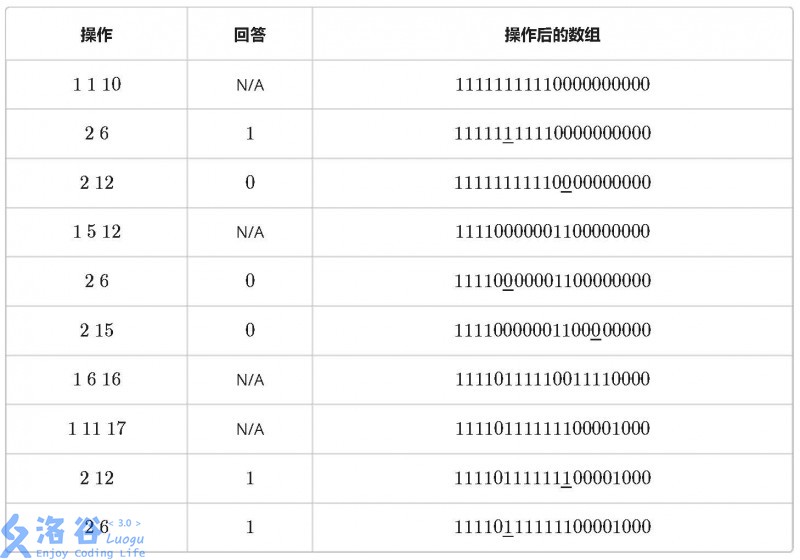
输入输出格式

输入格式：

第一行包含两个整数 n, m，表示数组的长度和指令的条数； 以下 m 行，每行的第一个数 t 表示操作的种类：

若 t = 1，则接下来有两个数 L, R，表示区间 [L, R] 的每个数均反转； 若 t = 2，则接下来只有一个数 i，表示询问的下标。

输出格式：

每个操作 2 输出一行（非 0 即 1），表示每次操作 2 的回答。

输入输出样例

输入样例#1：

20 10
1 1 10
2 6
2 12
1 5 12
2 6
2 15
1 6 16
1 11 17
2 12
2 6

输出样例#1：

1
0
0
0
1
1

说明

对于 50% 的数据，1 ≤ n ≤ 10^3, 1 ≤ m ≤ 10^4； 对于 100% 的数据，1 ≤ n ≤ 10^5, 1 ≤ m ≤ 5 × 10^5，保证 L ≤ R。

线段树的区间修改，单点查询，似乎并不用建树，建树好像还有问题

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+;
int xxoo[maxn];
int n,m,L,R,opt,x;
void pushdown(int now)
{
    if(xxoo[now])
    {
        xxoo[now*]^=;
        xxoo[now*+]^=;
        xxoo[now]=;
    }
}
void modify(int now,int l,int r,int stdl,int stdr)
{
    if(stdl>=l&&stdr<=r)
    {
        xxoo[now]^=;
        return;
    }
    pushdown(now);
    int mid=(stdl+stdr)>>;
    if(l<=mid)
    {
        modify(now<<,l,r,stdl,mid);
    }
    if(r>mid)
    {
        modify(now<<|,l,r,mid+,stdr);
    }
}
int query(int now,int x,int stdl,int stdr)
{
    if(stdl==stdr)
    {
        return xxoo[now];
    }
    pushdown(now);
    int mid=(stdl+stdr)>>;
    if(x<=mid)
    {
        return query(now<<,x,stdl,mid);
    }
    else
    {
        return query(now<<|,x,mid+,stdr);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        scanf("%d",&opt);
        if(opt==)
        {
            scanf("%d%d",&L,&R);
            modify(,L,R,,n);
        }
        else
        {
            scanf("%d",&x);
            printf("%d\n",query(,x,,n));
        }
    }
    return ;
}

错误代码(多了一个建树)

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+;
struct node
{
    int l;
    int r;
    int lazyxor;
    int value;
    int sum;
}tree[maxn*];
int n,m,L,R,opt,x;
void build(int now,int l,int r)
{
    tree[now].l=l;
    tree[now].r=r;
    tree[now].lazyxor=;
    if(l==r)
    {
        tree[now].value=tree[now].sum=;
        return;
    }
    int mid=(l+r)>>;
    build(now<<,l,mid);
    build(now<<|,mid+,r);
    tree[now].sum=tree[now*].sum+tree[now*+].sum;
}
void pushdown(int now)
{
    if(tree[now].lazyxor)
    {
        tree[now*].lazyxor^=;
        tree[now*+].lazyxor^=;
        tree[now].lazyxor=;
    }
}
void modify(int now,int l,int r)
{
    if(tree[now].l>=l&&tree[now].r<=r)
    {
        tree[now].lazyxor^=;
        return;
    }
    pushdown(now);
    int mid=(tree[now].l+tree[now].r)>>;
    if(l<=mid)
    {
        modify(now<<,l,mid);
    }
    if(r>mid)
    {
        modify(now<<|,mid+,r);
    }
}
int query(int now,int x,int l,int r)
{
    if(tree[now].l==tree[now].r)
    {
        return tree[now].lazyxor;
    }
    pushdown(now);
    int mid=(tree[now].l+tree[now].r)>>;
    if(x<=mid)
    {
        return query(now*,x,l,r);
    }
    else
    {
        return query(now*+,x,l,r);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    build(,,n);
    for(int i=;i<=m;i++)
    {
        scanf("%d",&opt);
        if(opt==)
        {
            scanf("%d%d",&L,&R);
            modify(,L,R);
        }
        else
        {
            scanf("%d",&x);
            printf("%d\n",query(,x,,n));
        }
    }
    return ;
}