sklearn中的pipeline实际应用

前面提到，应用sklearn中的pipeline机制的高效性；本文重点讨论pipeline与网格搜索在机器学习实践中的结合运用：

结合管道和网格搜索以调整预处理步骤以及模型参数

一般地，sklearn中经常用到网格搜索寻找应用模型的超参数；实际上，在训练数据被送入模型之前，对数据的预处理中也会有超参数的介入，比如给数据集添加多项式特征时所指定的指数大小；

而且，一般都是将数据预处理完成后再传入估计器进行拟合，此时利用网格搜索只会单独调整估计器的超参数；如若利用pipeline结合预处理步骤和模型估计器则可以同时寻找最佳的超参数配对。

实例如下：

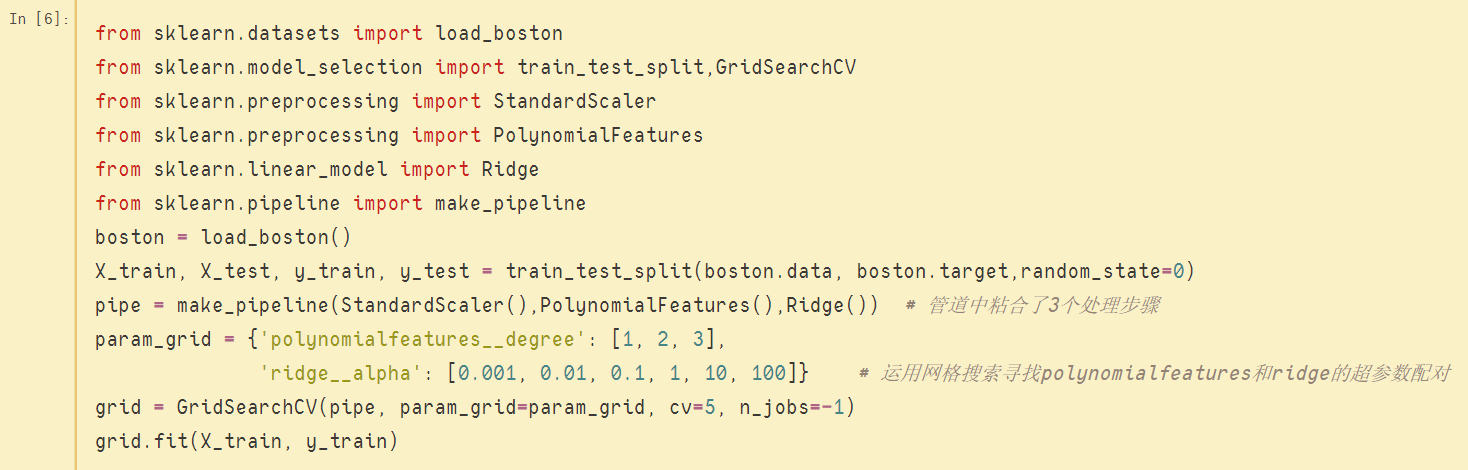
上图中，利用管道结合了3个处理步骤，并使用网格搜索机制针对其中两个步骤的超参数进行调优，一个是预处理阶段的PolynomialFeatures，另一个是模型Ridge

结合管道和网格搜索以选定模型

一般地，选用不同的模型会涉及到不同的预处理步骤，如采用随机森林进行分类训练时可以不对数据作预处理操作，而应用支持向量机时则需要对数据进行标准化；

下图中，利用管道结合预处理中的标准化步骤和分类模型，当模型采用随机森林时，预处理步骤置空，并利用网格搜索寻找随机森林的超参数；当模型采用支持向量机时，启用预处理步骤，并利用网格搜索寻找支持向量机的超参数。

通过此种结合应用，选定最适合的分类模型。