学习：多项式算法----FWT

FWT也称快速沃尔什变换，是用来求多项式之间位运算的系数的。FWT的思想与FFT有异曲同工之妙，但较FFT来说，FWT比较简单。

前言

---

之前学习FFT（快速傅里叶变换）的时候，我们知道FFT是用来快速求两个多项式乘积的，即求序列C：

$$C_k=\sum_{i+j=k}A_iB_j$$

而FWT解决的多项式的位运算，即知道两个序列A与B，求：

$$C_k=\sum_{i\&j=k}A_iB_j\;\;(\& 表示位运算"与")$$

$$C_k=\sum_{i|j=k}A_iB_j\;\;(| 表示位运算"或")$$

$$C_k=\sum_{i\land j=k}A_iB_j\;\;(\land 表示位运算"异或")$$

如图FFT的解决方法，在FWT中，我们需要找到一种线性变换$FWT$，使得原序列$A$变成一个新的序列$FWT(A)$，新序列与由原序列线性相关。

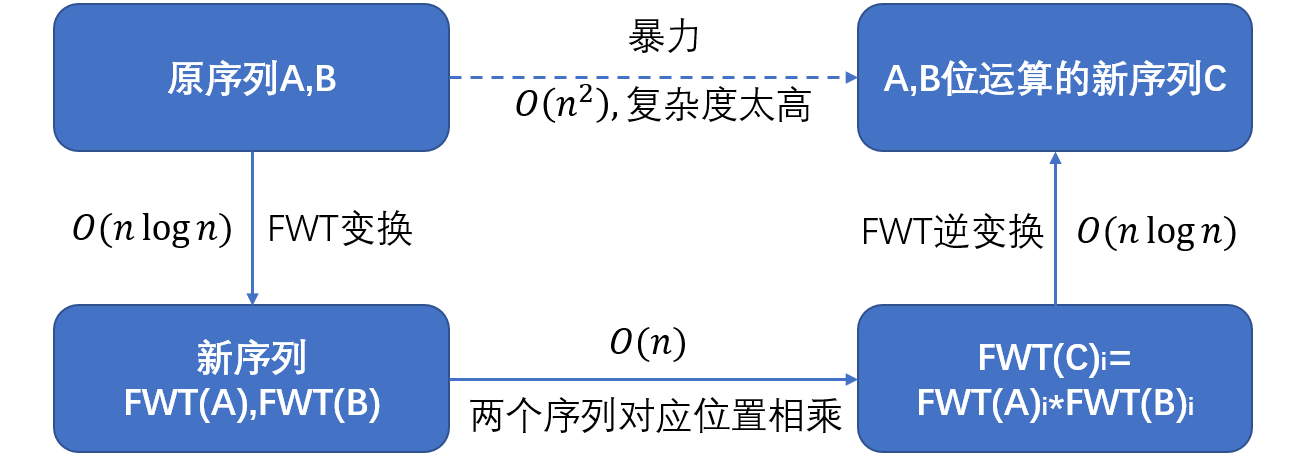
注意，由于FWT变换是一种线性变换，所以一定满足

$$FWT(A)+FWT(B)=FWT(A+B)$$

与FFT一样，我么需要把序列用0补成2的幂次方个，然后分割成序列为2的区间，然后更新数值，再合并，再一段段更新，再合并....直到最后合并成一个序列，然后进行最后一次更新即可得到变换后的序列。

---

FWT_OR

---

已知两个序列A，B，求新的序列C，其中

$$C=\left\{\sum_{i|j=0}A_iB_j,\sum_{i|j=1}A_iB_j,\sum_{i|j=2}A_iB_j,...\right\}$$

故

$$C_k=\sum_{i|j=k}A_iB_j$$

假设序列为$A$，前一半元素（前$2^{n-1}$个）元素组成的序列为$A_0$，后一半元素（后$2^{n-1}$个）元素组成的序列为$A_1$，故$A=(A_0,A_1)$

若序列A的长度为$2^n$，更新方法：

$$FWT(A)=\begin{cases}A&n=0\\(FWT(A_0),FWT(A_0)+FWT(A_1))&n>0\end{cases}$$

","表示合并前后两个序列。

此时可以证明$$FWT(C)=FWT(A|B)=FWT(A)*FWT(B)$$

借某位大佬的证明方法：

$FWT(A|B)=FWT((A|B)_0,(A|B)_1)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =FWT(A_0|B_0,A0|B_1+A_1|B0+A_1|B_1)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0|B_0),FWT(A_0|B_0+A_0|B_1+A_1|B_0+A_1|B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0)×FWT(B_0),$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ FWT(A_0)×FWT(B_0)+FWT(A_0)×FWT(B_1)+$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ FWT(A_1)×FWT(B_0)+FWT(A_1)×FWT(B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0)×FWT(B_0),(FWT(A_0)+FWT(A_1))×$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (FWT(B_0)+FWT(B_1)))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0),FWT(A_0+A_1))×(FWT(B_0),FWT(B_0+B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =FWT(A)×FWT(B)$

然后对FWT(C)序列进行FWT逆变换（UFWT）即可得到C序列。

逆变换的更新方法可以根据正变换的形式得到，为

$$UFWT(A)=(UFWT(A_0),UFWT(A_1)-UFWT(A_0))$$

FWT或变换代码：

typedef long long ll;
void FWT_or(ll *a,int n){
    for(int i=;i<=n;i<<=)//i表示分治的区间
        for(int p=i>>,j=;j<n;j+=i)//p表示区间的一半，j表示区间开头
            for(int k=j;k<j+p;++k)//k来遍历每一个区间的前半部分
                a[k+p]+=a[k];//更新
    return;
}

UFWT或变换代码：

typedef long long ll;
void UFWT_or(ll *a,int n){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k)
                a[k+p]-=a[k];
    return;
}

合并代码：

void FWT_or(ll *a,int n,int opt){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k)
                a[k+p]+=a[k]*opt;
    return;
}

U/FWT_or

---

FWT_AND

---

已知两个序列A，B，求新的序列C，其中

$$C=\left\{\sum_{i\&j=0}A_iB_j,\sum_{i\&j=1}A_iB_j,\sum_{i\&j=2}A_iB_j,...\right\}$$

故

$$C_k=\sum_{i\&j=k}A_iB_j$$

假设序列为$A$，前一半元素（前$2^{n-1}$个）元素组成的序列为$A_0$，后一半元素（后$2^{n-1}$个）元素组成的序列为$A_1$，故$A=(A_0,A_1)$

若序列A的长度为$2^n$，更新方法：

$$FWT(A)=\begin{cases}A&n=0\\(FWT(A_0)+FWT(A_1),FWT(A_1))&n>0\end{cases}$$

","表示合并前后两个序列。

此时也可以证明$$FWT(C)=FWT(A\&B)=FWT(A)*FWT(B)$$

证明方法：

$FWT(A\&B)=FWT((A\&B)_0,(A\&B)_1)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =FWT(A_0\&B_0+A_0\&B_1+A_1\&B_0,A_1\&B_1)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0\&B_0+A_0\&B_1+A_1\&B_0+A_1\&B_1),FWT(A_1\&B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =((FWT(A0)+FWT(A1))×(FWT(B0)+FWT(B1)),FWT(A1)∗FWT(B1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A0+A1),FWT(A1))×(FWT(B0+B1),FWT(B1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =FWT(A)×FWT(B)$

然后对FWT(C)序列进行FWT逆变换（UFWT）即可得到C序列。

 

逆变换的更新方法可以根据正变换的形式得到，为

$$UFWT(A)=(UFWT(A_0)-UFWT(A_1),UFWT(A_1))$$

FWT与变换代码：

void FWT_and(ll *a,int n){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k)
                a[k]+=a[k+p];
    return;
}

UFWT或变换代码：

void UFWT_and(ll *a,int n){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k)
                a[k]-=a[k+p];
    return;
}

合并代码：

void FWT_and(ll *a,int n,int opt){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k)
                a[k]+=a[k+p]*opt;
    return;
}

U/FWT_and

---

FWT_XOR

---

已知两个序列A，B，求新的序列C，其中

$$C=\left\{\sum_{i\oplus j=0}A_iB_j,\sum_{i\oplus j=1}A_iB_j,\sum_{i\oplus j=2}A_iB_j,...\right\}$$

故

$$C_k=\sum_{i\oplus j=k}A_iB_j$$

假设序列为$A$，前一半元素（前$2^{n-1}$个）元素组成的序列为$A_0$，后一半元素（后$2^{n-1}$个）元素组成的序列为$A_1$，故$A=(A_0,A_1)$

若序列A的长度为$2^n$，更新方法：

$$FWT(A)=\begin{cases}A&n=0\\(FWT(A_0)+FWT(A_1),FWT(A_0)-FWT(A_1))&n>0\end{cases}$$

","表示合并前后两个序列。

此时仍然可以证明$$FWT(C)=FWT(A\oplus B)=FWT(A)*FWT(B)$$

证明方法：

$FWT(A⊕B)=(FWT(A⊕B)_0+FWT(A⊕B)_1,FWT(A⊕B)_0−FWT(A⊕B)_1)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0⊕B_0+A_1⊕B_1+A_1⊕B_0+A_0⊕B_1),$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ FWT(A_0⊕B_0+A_1⊕B_1−A_1⊕B_0−A_0⊕B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =((FWT(A_0)+FWT(A_1))×(FWT(B_0)+FWT(B_1)),$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (FWT(A_0)−FWT(A_1))×(FWT(B_0)−FWT(B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0+A_1)×(B_0+B_1),FWT(A_0−A_1)×FWT(B_0−B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =(FWT(A_0+A_1),FWT(A_0−A_1))×(FWT(B_0+B_1),FWT(B_0−B_1))$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =FWT(A)×FWT(B)$

然后对FWT(C)序列进行FWT逆变换（UFWT）即可得到C序列。

逆变换的更新方法可以根据正变换的形式得到，为

$$UFWT(A)=(\frac {UFWT(A_0)+UFWT(A_1)}2,\frac {UFWT(A_0)-UFWT(A_1)}2)$$

FWT异或变换代码：

void FWT_xor(ll *a,int n){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k){
                ll x=a[k],y=a[k+p];
                a[k]=x+y;a[k+p]=x-y;
            }
    return ;
}

UFWT变换代码：

void UFWT_xor(ll *a,int n){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k){
                ll x=a[k],y=a[k+p];
                a[k]=(x+y)/,a[k+p]=(x-y)/;
            }
    return ;
}

合并代码：

void FWT_xor(ll *a,int n,int opt){
    for(int i=;i<=n;i<<=)
        for(int p=i>>,j=;j<n;j+=i)
            for(int k=j;k<j+p;++k){
                ll x=a[k],y=a[k+p];
                if(opt==)    a[k]=x+y;a[k+p]=x-y;
                else    a[k]=(x+y)/,a[k+p]=(x-y)/;
            }
    return ;
}

U/FWT_xor

---

FWT异或变换的特殊作用

---

在FWT异或变换中，我们主要解决一个问题

$$h(i)=\sum_{j\oplus k=i}f(j)g(k)$$

根据某站某大佬的讲解，假设存在三个集合$L,R,S$满足

$$h(S)=\sum_{R\oplus L=i}f(R)g(L)$$

则为了解决快速多项式异或，我们需要将上面的式子变形。

首先介绍一个等式，假设全集为U，集合内有n个元素，其中$|T|$表示集合T的大小，则

$$\frac 1{2^n}\sum_{T\subseteq U}(-1)^{|W\cap T|}=1$$

上面的式子仅在$W=\varnothing$时成立

解释一下：由于集合$T$是集合$U$的子集，故集合$T$有$2^n$中可能，一旦$W$不是空集，$(-1)^{|W\cap T|}$就可能等于1，那么$\sum_{T\subseteq U}(-1)^{|W\cap T|}$就会小于$2^n$。所以只有当$W$是空集时，上面式子才等于1

有了上面的等式，就可以变形了，由于$R\oplus L=S$，故$R\oplus L\oplus S=\varnothing$

$$h(S)=\sum_{R\oplus L=i}f(R)g(L)$$

$$=\sum_{R\subseteq U}\sum_{L\subseteq U}[R\oplus L\oplus S=\varnothing]f(L)g(R)$$

$$=\sum_{R\subseteq U}\sum_{L\subseteq U}\frac 1{2^n}\sum_{T\subseteq U}(-1)^{|R\oplus L\oplus S\cap T|}f(L)g(R)$$

下面证明$|T\cap \oplus^{n}_{i=1}S_i|$与$\sum_{i=1}^n|S_i\cap T|$的奇偶性相同，先证明n=2的情况：

假设$|T\cap S_1|=A,|T\cap S_2|=B$

1.假设$T\cap S_1$与$T\cap S_2$没有相同位的数相同，那么：

$$(-1)^{\sum_{i=1}^2|S_i\cap T|}=(-1)^{|S_1\cap T|+|S_2\cap T|}=(-1)^{A+B}=(-1)^{|T\cap (S_1\oplus S_2)|}$$

2.假设$T\cap S_1$与$T\cap S_2$有x组相同位的数相同，那么：

$$(-1)^{\sum_{i=1}^2|S_i\cap T|}=(-1)^{|S_1\cap T|+|S_2\cap T|}=(-1)^{A+B}$$$$(-1)^{|T\cap (\oplus_{i=1}^2S_i)|}=(-1)^{|T\cap (S_1\oplus S_2)|}=(-1)^{A+B-2x}=(-1)^{A+B}$$

当然n等于任何数的时候也是像上面一样可以证明的，所以$$(-1)^{|R\oplus L\oplus S\cap T|}=(-1)^{|R\cap T|+|S\cap T|+|L\cap T|}$$

故上面式子继续变形可得

$$\frac 1{2^n}\sum_{L\subseteq U}\sum_{R\subseteq U}\sum_{T\subseteq U}(-1)^{|L\cap T|}(-1)^{|R\cap T|}(-1)^{|S\cap T|}f(R)g(L)$$

于是发现了FWT_xor变形的本质，即变形后的序列$f(T)$与变形前序列$f(R)$的关系

$$f(T)=\sum_{R\subseteq U}(-1)^{|R\cap T|}f(R)$$

通过以上的探究，得到结论：假设原序列为A，变形后的序列为A'，那么

$$A'[x]=\sum_{|x\&i|\bmod {2}=0}A[i]-\sum_{|x\&i|\bmod {2}\neq 0}A[i]$$

---

例题

---

1.2019牛客暑期多校训练营（第一场）----D-Parity of Tuples：https://blog.csdn.net/weixin_43702895/article/details/97114770