机器学习：SVM（非线性数据分类：SVM中使用多项式特征和核函数SVC）

一、基础理解

• 数据：线性数据、非线性数据；
• 线性数据：线性相关、非线性相关；（非线性相关的数据不一定是非线性数据）

　1）SVM 解决非线性数据分类的方法

• 方法一：

• 多项式思维：扩充原本的数据，制造新的多项式特征；（对每一个样本添加多项式特征）
• 步骤：

1. PolynomialFeatures(degree = degree)：扩充原始数据，生成多项式特征；
2. StandardScaler()：标准化处理扩充后的数据；
3. LinearSVC(C = C)：使用 SVM 算法训练模型；

• 方法二：

• 使用scikit-learn 中封装好的核函数： SVC(kernel='poly', degree=degree, C=C)
• 功能：当 SVC() 的参数 kernel = ‘poly’ 时，直接使用多项式特征处理数据；

• 注：使用 SVC() 前，也需要对数据进行标准化处理

二、例

　1）生成数据

• datasets.make_ + 后缀：自动生成数据集；
• 如果想修改生成的数据量，可在make_moons()中填入参数；

  import numpy as np
  import matplotlib.pyplot as plt
  from sklearn import datasets
  
  X, y = datasets.make_moons(noise=0.15, random_state=666)
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()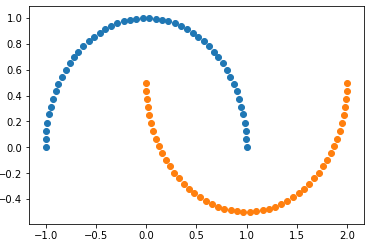

  

　2）绘图函数

• def plot_decision_boundary(model, axis):
  
      x0, x1 = np.meshgrid(
          np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
          np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
      )
      X_new = np.c_[x0.ravel(), x1.ravel()]
  
      y_predict = model.predict(X_new)
      zz = y_predict.reshape(x0.shape)
  
      from matplotlib.colors import ListedColormap
      custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
  
      plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

　3）方法一：多项式思维

• from sklearn.preprocessing import PolynomialFeatures, StandardScaler
  from sklearn.svm import LinearSVC
  from sklearn.pipeline import Pipeline
  
  def PolynomialSVC(degree, C=1.0):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std)scaler', StandardScaler()),
          ('linearSVC', LinearSVC(C=C))
      ])
  
  poly_svc = PolynomialSVC(degree=3)
  poly_svc.fit(X, y)
  
  plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()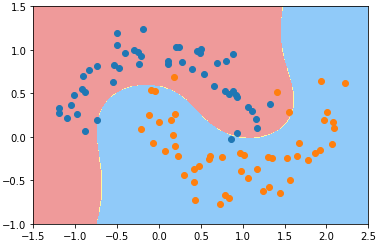

  

• 改变参数：degree、C，模型的决策边界也跟着改变；

　4）方法二：使用核函数 SVC()

• 对于SVM算法，在scikit-learn的封装中，可以不使用 PolynomialFeatures的方式先将数据转化为高维的具有多项式特征的数据，在将数据提供给算法;
• SVC() 算法：直接使用多项式特征；

  from sklearn.svm import SVC
  
  # 当算法SVC()的参数 kernel='poly'时，SVC()能直接打到一种多项式特征的效果；
  # 使用 SVC() 前，也需要对数据进行标准化处理
  def PolynomialKernelSVC(degree, C=1.0):
      return Pipeline([
          ('std_scaler', StandardScaler()),
          ('kernelSVC', SVC(kernel='poly', degree=degree, C=C))
      ])
  
  poly_kernel_svc = PolynomialKernelSVC(degree=3)
  poly_kernel_svc.fit(X, y)
  
  plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
  plt.scatter(X[y==0, 0], X[y==0, 1])
  plt.scatter(X[y==1, 0], X[y==1, 1])
  plt.show()

  

• 调整 PolynomialkernelSVC() 的参数：degree、C，可改决策边界；