机器学习五 -- 机器学习的“Hello World”，感知机

机器学习五 -- 机器学习的“Hello World”，感知机

感知机是二类分类的线性分类模型，是神经网络和支持向量机的基础。其输入为实例的特征向量，输出为实例的类别，取+1和-1二值之一，即二类分类。感知机对应于输入空间（特征空间）将实例划分为正负两类的分离超平面，属于判别模型。我们对于感知机的学习旨在求出将训练数据进行线性划分的分离超平面，为此目标，我们需要导入基于误分类的损失函数，利用后文所提到的梯度下降法对损失函数进行极小化，求得感知机模型。

感知机模型

对此我们都知道了什么叫感知机了。这里给出一个比较数理化的定义：假设输入空间（特征空间）是XєRⁿ,输出空间是Y={+1,-1}。输入xєX表示实例的特征向量，对应于输入空间的点，输出yєY表示实例的类别。由输入空间到输出空间的如下函数

f(x)=sign(w*x+b)

称为感知机。其中，w和b为感知机模型参数，wєRⁿ叫做权值或权值向量，bєR叫做偏置，w·x表示w和x的内积，sign是符号函数，即为

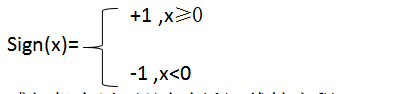
感知机有以下几何解释：线性方程w·x+b=0对应于特征空间Rn的一个超平面S，其中w是超平面的法向量，b是超平面的截距。这个超平面将特征空间划分为两个部分，位于两部分的点分别被称为正、负两类。因此，超平面S即被称为分离超平面。

感知机学习策略

给定一个数据集合T={(x1,y1)，(x2,y2)，……,(xn,yn)}，其中xiєX=R^_n，yiєY={+1,-1}，i=1,2,3,,,,n，如果存在某个超平面S：w·x+b=0能够将数据集的正实例点和负实例点完全正确的划分到超平面的两侧，即对所有yi=+1的实例点，有w·xi+b>0,对所有yi=-1的实例点，有w·xi+b<0，则称数据集T为线性可分数据集；否则，称数据集T为线性不可分。

刚才我们有提到，我们感知机学习的目标就是求得一个能够将训练集正实例和负实例点完全正确分开，为了找到这样一个分离超平面，我们需要定义损失函数并将损失函数极小化。

给定一个数据集合T={(x1,y1)，(x2,y2)，……,(xn,yn)}，其中xiєX=Rn，yiєY={+1,-1}，i=1,2,3,,,,n，感知机sign(w·x+b)学习的损失函数定义为

L(w,b) = -∑yi(w·xi+b)(xiєM)

其中M为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。

想一想：是不是可以肯定损失函数L（w,b）是非负的，为什么？

感知机学习算法

感知机学习算法转化为求解损失函数式子的最优化问题，下面简单介绍一下两个具体的算法：原始形式和对偶形式。

感知机学习的原始形式

感知机学习算法是误分类驱动的，如果我们人类逼格够高，给出任意一个线性可分数据集，可以马上脑补出一个将其数据集完全正确分类的模型，那么就用不着感知机学习算法了。所以，我们需要用算法来尽可能的优化函数来达到期望目标。其方法具体采用了随机梯度下降法。首先，任意选取一个超平面w0,b0，然后用梯度下降法不断的极小化目标函数，极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其下降。

输入：训练数据集T={(x1,y1)，(x2,y2)，……,(xn,yn)}，其中xiєX=Rn，yiєY={+1,-1}，i=1,2,3,,,,n；学习率η(0<η<=1)；

输出：w,b；感知机模型f(x)=sign(w·x+b)。

（1）选取初值w0,b0;

（2）在训练集中选取数据(xi,yi)

（3）如果yi(w·xi+b)<=0

w ← w+ηyixi   b ← b+ηyi

（4）转至（2），直至训练集中没有误分类点

感知机学习的对偶形式

对偶形式的基本想法是：将w和b表示为实例xi和标记yi的线性组合的形式，通过求解其系数而求得w和b。

刚才说到如果yi(w·xi+b)<=0，那么w ← w+ηyixi   b ← b+ηyi

假设修改了n次，则w,b关于（xi,yi）的增量分别是αiyixi和αiyi，这里αi=niη。

输入：训练数据集T={(x1,y1)，(x2,y2)，……,(xn,yn)}，其中xiєX=Rn，yiєY={+1,-1}，i=1,2,3,,,,n；学习率η(0<η<=1)；

输出：α,b:感知机模型f(x)=sign{∑αjyjxj·x+b}(1<=j<=N)

其中α=（α1，α2，，，αn）T

（1）α ← 0 , b←0

（2）在训练集中选取数据(xi,yi)

（3）如果yi(∑αjyjxj·x+b（1<=j<=N））<=0

ai ← ai+η  b ← b+ηyi

（4）转至（2）直到没有误分类数据。