【题解】HAOI2008硬币购物

1A什么的实在是太开心啦~~洛谷P1450

这道题目主要是考察对于容斥原理的掌握。

首先，注意到如果不存在有关硬币数量的限制而单纯询问方案的总数，就是一个简单的完全背包。这个思路提醒我们：如果能够求出所有不合法的方案，是不是就可以相减得到我们想要的答案了呢？那么我们注意到：令A[i]为第i种硬币超出范围的方案总数，显然有A[i]=dp[s-(d[i]+1)*c[i]]：强行超出，注意d[i]+1因为可以达到d[i]；剩下的就套容斥原理的公式即可：

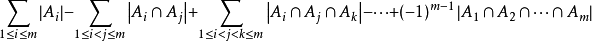
代码：

#include <bits/stdc++.h>
using namespace std;
#define V 100000
#define ll long long
int s, c[], T, a[], d[];;
ll dp[V + ];
int read()
{
    int x = ;
    char c;
    c = getchar();
    while(c < '' || c > '') c = getchar();
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x;
}

ll Get_Ans()
{
    ll ans = ;
    for(int i = ; i <= ; i ++)
        a[i] = (d[i] + ) * c[i];
    for(int i = ; i <= ; i ++)
        if(a[i] <= s) ans += dp[s - a[i]];
    for(int i = ; i <= ; i ++)
        for(int j = i + ; j <= ; j ++)
            if((a[i] + a[j]) <= s) ans -= dp[s - a[i] - a[j]];
    for(int i = ; i <= ; i ++)
        for(int j = i + ; j <= ; j ++)
            for(int k = j + ; k <= ; k ++)
                if(a[i] + a[j] + a[k] <= s) ans += dp[s - a[i] - a[j] - a[k]];
    if(a[] + a[] + a[] + a[] <= s) ans -= dp[s - a[] - a[] - a[] - a[]];
    return dp[s] - ans;
}

int main()
{
    for(int i = ; i <= ; i ++) c[i] = read();
    T = read();
    dp[] = ;
    for(int i = ; i <= ; i ++)
        for(int j = c[i]; j <= V; j ++)
            dp[j] += dp[j - c[i]];
    for(int i = ; i <= T; i ++)
    {
        for(int j = ; j <= ; j ++) d[j] = read();
        s = read();
        printf("%lld\n", Get_Ans());
    }
    return ;
}