B1277 [HNOI2002]Tinux系统树形dp

这个题bzoj上没有图，luogu上样例有问题。。。其实这个题代码不难，但是思考起来还是有一定难度的，其实这些题的重点都在于思考。我就不写了，洛谷上唯一的题解写的挺好，大家可以看一看。

题干：

在dos系统诞生以前，美国曾研究出一种类似的操作系统，名为Tinux系统。但由于硬件设施的制约，Tinux系统有许多的缺点。下面就对Tinux系统作一个简单的介绍：

Tinux系统是Tiger博士为美国军方研制开发的一种操作系统，该系统对文件的存储方式类似于dos系统，像一棵树一样，每一个叶子节点表示一个文件，每一个非叶子节点表示一个目录。其中定义i级子目录表示从根目录开始访问，一直访问到该子目录（不包括该子目录）需要访问的目录的个数为i的目录，所以根目录下的目录为一级子目录，其他的目录以此类推。但是在同一子目录下，受到硬件的制约Tinux系统最多只能够存储k个文件或子目录，也就是说这棵树里面的每一个非叶子节点最多只有k个子节点。这样就导致在文件数量较多的情况下，访问存储在该系统当中的文件A，往往要先访问一系列的子目录，我们称这些子目录为文件A的上级目录。例如下面这一个例子：

Root  A1

 A2

 A3

 A4

 A4A1

 A4A2

 A4A2A1

 A4A2A2

 A4A3

当我们要访问文件A4A2A1时就必须先访问它的上级目录：一级子目录A4和二级子目录A4A2。

Tinux系统在存储文件时，给每一个子目录都分配了k个指针，分别指向存放在该目录下的每一个文件和每一个目录，因此对文件的访问实质上就是对指针的访问。但是由于硬件原因，这k个指针不尽相同，因此访问它们的时间也不同，访问第i个指针所耗费的时间为。但是对于两个不同的子目录（不管它们各自属于哪一级目录）而言它们各自所拥有的k个指针是相同的。

Tinux系统最大的缺点是访问一个目录时，必须把该目录下所有的文件读入到内存当中来，这些文件包括在其各级子目录当中的文件，例如上面那一个例子，访问A4那一个目录，就必须把A4A1，A4A2A1，A4A2A2，A4A3这四个文件都读入到内存当中来，访问一个目录所需要的时间为（x表示该目录及其各级子目录下文件的个数，表示指向该目录的指针的访问时间）。因此根据上面介绍的访问方法，单独访问一个文件所需要的总时间为访问其所有上级目录（不包括根目录）所需要的时间与访问指向该文件的指针所需要的时间的和，例如上面那一个例子，访问文件A4A2A1需要的时间=访问目录A4的时间+访问目录A4A2的时间+访问指向文件A4A2A1的指针需要的时间。

现在，tiger博士准备将n个文件存储到一个空的Tinux系统当中，希望你帮助他设计一个程序找到一种最优的存储方法，使得单独访问这n个文件所需要的时间总和最小。

输入输出格式

输入格式：

输入由文件”system.in”读入。

文件的第一行为两个正整数，，接下来的k行每行有一个正整数。

输出格式：

输出到文件”system.out”，输出文件仅有一个正整数，表示在最优存储方案下，单独访问这n个文件所需要的时间总和。（结果小于2的31次方）

输入输出样例

输入样例#1：
复制

输出样例#1： 复制

说明

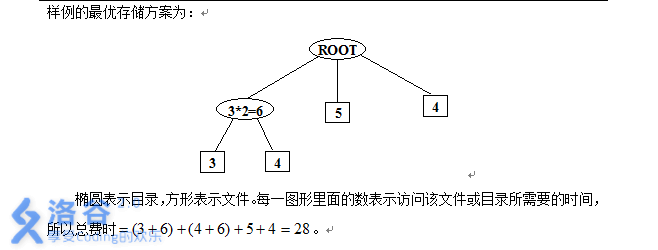
代码：

#include<iostream>

#include<cstdio>

#include<cmath>

#include<ctime>

#include<queue>

#include<algorithm>

#include<cstring>

using namespace std;

#define duke(i,a,n) for(int i = a;i <= n;i++)

#define lv(i,a,n) for(int i = a;i >= n;i--)

#define clean(a) memset(a,0,sizeof(a))

const int INF =  << ;

typedef long long ll;

typedef double db;

template <class T>

void read(T &x)

{

    char c;

    bool op = ;

    while(c = getchar(), c < '' || c > '')

        if(c == '-') op = ;

    x = c - '';

    while(c = getchar(), c >= '' && c <= '')

        x = x *  + c - '';

    if(op) x = -x;

}

template <class T>

void write(T x)

{

    if(x < ) putchar('-'), x = -x;

    if(x >= ) write(x / );

    putchar('' + x % );

}

int f[][];

int n,k,p[];

int MIN(int x,int y)

{

    if(!x)

    return y;

    else

    return min(x,y);

}

int dp(int x,int y,int l)

{

    if(x == )

    {

        f[x][y] = p[y];

        return f[x][y];

    }

    if(y == k)

    {

        f[x][y] = p[y] * x * x + dp(x,,x - );

        return f[x][y];

    }

    int tmp = k - y + ;

    if(tmp * l < x)

    return INF;

    if(f[x][y]) return f[x][y];

    tmp = (x - ) / tmp + ;

    duke(i,tmp,l)

    {

        if(i == )

            f[x][y] = p[y] + dp(x - ,y + ,x - );

        else

            f[x][y] = MIN(f[x][y],dp(x - i,y + ,x - i - ) + dp(i,,i - ) + p[y] * i * i);

    }

    return f[x][y];

}

int main()

{

    read(n);read(k);

    duke(i,,k)

    read(p[i]);

    sort(p + ,p + k + );

    printf("%d\n",dp(n,,n - ));

    return ;

}