机器学习优化方法总结比较（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）

SGD:

此处的SGD指mini-batch gradient descent，关于batch gradient descent, stochastic gradient descent, 以及 mini-batch gradient descent的具体区别就不细说了。现在的SGD一般都指mini-batch gradient descent。

SGD就是每一次迭代计算mini-batch的梯度，然后对参数进行更新，是最常见的优化方法了。即：

其中，是学习率，是梯度。 SGD完全依赖于当前batch的梯度，所以可理解为允许当前batch的梯度多大程度影响参数更新

缺点：

• 选择合适的learning rate比较困难 - 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征，有时对于不经常出现的特征我们可能想更新快一些，对于常出现的特征更新慢一些，这时候SGD就不太能满足要求了
• SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点

梯度下降(其他的line search、trust region也一样)只有在原问题是凸问题的情况下，才能保证以任意精度(因为毕竟是数值方法)取得最优解。

非凸情况下，当有多个极大值或极小值时，需要对梯度下降进行优化，比如动量，NAG，Adagrad，RMSprop等，可以减少陷入极大值极小值的可能性，设置得当可以得到全局最优解，但并不能100%保证获得全局最优解。

Momentum:

momentum是模拟物理里动量的概念，更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向，可以在一定程度上增加稳定性，从而学习更快，并且还有摆脱局部最优的能力。公式如下：

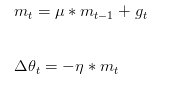
其中，是动量因子

特点：

• 下降初期时，使用上一次参数更新，下降方向一致，乘上较大的能够进行很好的加速
• 下降中后期时，在局部最小值来回震荡的时候，，使得更新幅度增大，跳出陷阱
• 在梯度改变方向的时候，能够减少更新 总而言之，momentum项能够在相关方向加速SGD，抑制振荡，从而加快收敛

Adagrad:

同一个更新速率不一定适合所有参数，比如有的参数可能已经到了仅需要微调的阶段，但又有些参数由于对应样本少等原因，还需要较大幅度的调动。Adagrad其实是对学习率进行了一个约束,每次迭代过程中，每个参数优化时使用不同的学习率。即：

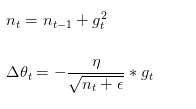
此处，对从1到进行一个递推形成一个约束项regularizer，，用来保证分母非0

特点：

• 前期较小的时候， regularizer较大，能够放大梯度
• 后期较大的时候，regularizer较小，能够约束梯度
• 适合处理稀疏梯度

缺点：

• 由公式可以看出，仍依赖于人工设置一个全局学习率
• 设置过大的话，会使regularizer过于敏感，对梯度的调节太大
• 中后期，分母上梯度平方的累加将会越来越大，使，使得训练提前结束

Adadelta:

Adadelta是对Adagrad的扩展，最初方案依然是对学习率进行自适应约束，但是进行了计算上的简化。 Adagrad会累加之前所有的梯度平方，Adadelta只使用adagrad的分母中的累计项离当前时间点比较近的项。即：

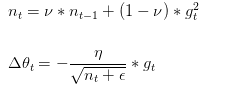
在此处Adadelta其实还是依赖于全局学习率的，但是作者做了一定处理，经过近似牛顿迭代法之后：

其中，代表求期望。

此时，可以看出Adadelta已经不用依赖于全局学习率了。

Adam:

Adam(Adaptive Moment Estimation)是一种不同参数自适应不同学习速率方法，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。公式如下：

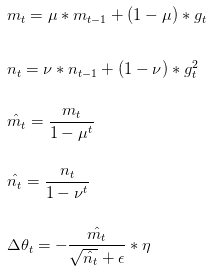
$m_t, n_t$分别是梯度的带权平均和带权有偏方差，初始为0向量，Adam的作者发现他们倾向于0向量(接近于0向量)，特别是在衰减因子(衰减率)$\mu ,  \nu$接近于1时,所以要进行偏差修正，，是对，的校正。

论文中建议：$\mu = 0.9, \nu = 0.999, \epsilon = 10^{-8}$

特点：

• 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
• 对内存需求较小
• 为不同的参数计算不同的自适应学习率
• 也适用于大多非凸优化 - 适用于大数据集和高维空间

经验之谈

• 对于稀疏数据，尽量使用学习率可自适应的优化方法，不用手动调节，而且最好采用默认值
• SGD通常训练时间更长，但是在好的初始化和学习率调度方案的情况下，结果更可靠
• 如果在意更快的收敛，并且需要训练较深较复杂的网络时，推荐使用学习率自适应的优化方法。

http://blog.csdn.net/heyongluoyao8/article/details/52478715

https://zhuanlan.zhihu.com/p/22252270

牛顿法  拟牛顿法的实现

http://blog.csdn.net/golden1314521/article/details/46225289

---

https://arxiv.org/pdf/1706.10207.pdf