洛谷 P2611 [ZJOI2012]小蓝的好友 解题报告

P2611 [ZJOI2012]小蓝的好友

题目描述

终于到达了这次选拔赛的最后一题，想必你已经厌倦了小蓝和小白的故事，为了回馈各位比赛选手，此题的主角是贯穿这次比赛的关键人物——小蓝的好友。

在帮小蓝确定了旅游路线后，小蓝的好友也不会浪费这个难得的暑假。与小蓝不同，小蓝的好友并不想将时间花在旅游上，而是盯上了最近发行的即时战略游戏——SangoCraft。但在前往通关之路的道路上，一个小游戏挡住了小蓝的好友的步伐。

“国家的战争其本质是抢夺资源的战争”是整款游戏的核心理念，这个小游戏也不例外。简单来说，用户需要在给定的长方形土地上选出一块子矩形，而系统随机生成了N个资源点，位于用户所选的长方形土地上的资源点越多，给予用户的奖励也越多。悲剧的是，小蓝的好友虽然拥有着极其优秀的能力，但同时也有着极差的RP，小蓝的好友所选的区域总是没有一个资源点。

终于有一天，小蓝的好友决定投诉这款游戏的制造厂商，为了搜集证据，小蓝的好友想算出至少包含一个资源点的区域的数量。作为小蓝的好友，这自然是你分内之事。

输入输出格式

输入格式：

每个输入文件中仅包含一个测试数据。

第一行包含由两个空格隔开的正整数\(R\),\(C\),\(N\)，表示游戏在一块\([1,R] \times [1,C]\)的地图上生成了\(N\)个资源点。

接下来有\(N\)行，每行包含两个整数 \(x,y\)，表示这个资源点的坐标

\((1 \le x \le r,1 \le y \le C)\)

输出格式：

输出文件应仅包含一个整数，表示至少包含一个资源点的区域的数量。

具体的说，设\(N\)个资源点的坐标为\((i=1..n)\),你需要计算有多少个四元组\((L_B,D_B,R_B,U_B)\)满足\(1<=L_B<=R_B<=R,1<=D_B<=U_B<=C\)，且存在一个\(i\)使得 \(L_B<=x_i<=R_B,D_B<=y_i<=U_B\)均成立。

说明

对于\(20\%\)的数据，\(N<=50\)。

对于\(40\%\)的数据，\(N<=2000\)。

对于\(100\%\)的数据，\(R,C<=40000,N<=100000\)，资源点的位置两两不同，且位置为随机生成。

---

我们首先弄清楚我们咋统计的

先把矩形蓝白出来

然后我们对矩形固定一个下边界，设为\(down\)

然后我们枚举所取矩形的左边界与右边界

如何不重不漏的把所有可行上边界统计呢？

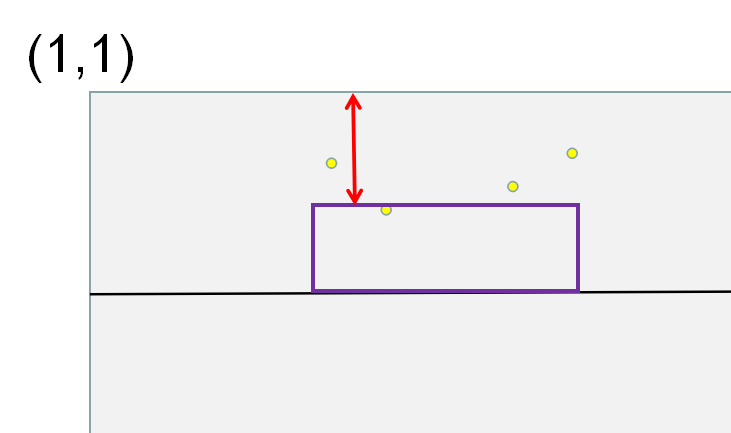
比方说，黑线是矩形下边界，左右边界现在是任意枚举的，那么红色箭头范围内就是上边界可取的集合了

我们发现，上边界的最下取值点与最低的那个点相连

那么我们可以枚举每个左右边界，然后找到最低的那个点，我们就得到了一个优秀的\(O(N^4)\)的解法辣

注：这里把矩形规模称作\(N\)，把点的个数称作\(K\)

取最低点的优化很容易搞成\(O(N^3)\)的，然而这样布星。

---

我们像CDQ分治那样进行统计

具体的，对每一个固定的下边界，每一列都有唯一确定的最低的点

我们以第\(x\)列的\(x\)为二叉排序树的关键字，以那个最低的点的行数\(y\)为大根堆的关键字，建立一颗\(treap\)

在统计每一个固定的下边界时，每个点的贡献都是 (左儿子大小+1)\(\times\) (右儿子大小+1) \(\times\) 堆的关键字

表示，左边区间可取集合，右边区间可取集合和上边界可取集合

当然堆值可能会变，我们需要在改变的时候进行调整

这时候一个很显然的\(O(N^2)\)做法就有了

我们改完一行去遍历整棵树就可以了。

至于修改的复杂度，因为数据随机，可以看做是\(O(KlogN)\)的

如果我们对每个点维护它及它儿子的贡献，每次改的时候就只需要查询根节点就行辣

复杂度：\(O(KlogN)\)(数据随机)

---

Code:

#include <cstdio>
#include <algorithm>
#define ls ch[now][0]
#define rs ch[now][1]
#define fa par[now]
#define ll long long
const int N=1e5+10;
const int M=4e4+10;
int n,m,k;
std::pair <int,int > dx[N];
ll sum[M],dat[M],siz[M],ans;int ch[M][2],par[M],root;
int build(int l,int r)
{
    if(l>r) return 0;
    if(l==r) {siz[l]=1;return l;}
    int now=l+r>>1;
    ls=build(l,now-1);
    if(ls) par[ls]=now;
    rs=build(now+1,r);
    if(rs) par[rs]=now;
    siz[now]=siz[ls]+siz[rs]+1;
    return now;
}
void updata(int now)
{
    sum[now]=dat[now]*(siz[ls]+1ll)*(siz[rs]+1ll)+sum[ls]+sum[rs];
    siz[now]=siz[ls]+siz[rs]+1;
}
int identity(int now){return ch[fa][1]==now;}
void connect(int f,int now,int typ){fa=f;ch[f][typ]=now;}
void Rotate(int now)
{
    int p=fa,typ=identity(now);
    if(p==root) root=now;
    connect(p,ch[now][typ^1],typ);
    connect(par[p],now,identity(p));
    connect(now,p,typ^1);
    updata(p),updata(now);
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    root=build(1,m);
    for(int i=1;i<=k;i++)
        scanf("%d%d",&dx[i].first,&dx[i].second);
    std::sort(dx+1,dx+1+k);
    int las=1;dat[0]=n+1;
    for(int i=1;i<=k;i++)
    {
        while(las!=dx[i].first)
            ans+=sum[root],++las;
        int now=dx[i].second;
        dat[now]=dx[i].first;
        while(dat[fa]<dat[now])
            Rotate(now);
        while(now) updata(now),now=fa;
    }
    while(las<=n)
        ans+=sum[root],++las;
    printf("%lld\n",ans);
    return 0;
}

---

2018.8.26