【十大经典数据挖掘算法】AdaBoost

【十大经典数据挖掘算法】系列

1. C4.5
2. K-Means
3. SVM
4. Apriori
5. EM
6. PageRank
7. AdaBoost
8. kNN
9. Naïve Bayes
10. CART

---

1. 集成学习

集成学习（ensemble learning）通过组合多个基分类器（base classifier）来完成学习任务，颇有点“三个臭皮匠顶个诸葛亮”的意味。基分类器一般采用的是弱可学习（weakly learnable）分类器，通过集成学习，组合成一个强可学习（strongly learnable）分类器。所谓弱可学习，是指学习的正确率仅略优于随机猜测的多项式学习算法；强可学习指正确率较高的多项式学习算法。集成学习的泛化能力一般比单一的基分类器要好，这是因为大部分基分类器都分类错误的概率远低于单一基分类器的。

偏差与方差

“偏差-方差分解”（bias variance decomposition）是用来解释机器学习算法的泛化能力的一种重要工具。对于同一个算法，在不同训练集上学得结果可能不同。对于训练集\(D = \lbrace (x_1,y_1),(x_2,y_2), \cdots ,(x_N,y_N) \rbrace\)，由于噪音，样本\(x\)的真实类别为\(y_D\)（在训练集中的类别为\(y\)），则噪声为

\[
\xi^2 = \mathbb{E}_D[(y_d-y)^2]
\]

学习算法的期望预测为

\[
\bar{f}(x) = \mathbb{E}_D[f(x;D)]
\]

使用样本数相同的不同训练集所产生的方法

\[
var(x) = \mathbb{E}_D[ \left ( f(x;D) - \bar{f}(x) \right )^2]
\]

期望输入与真实类别的差别称为bias，则

\[
bias^2(x) = \left( \bar{f}(x) - y \right)^2
\]

为便于讨论，假定噪声的期望为0，即\(\mathbb{E}_D[y_d-y] = 0\)，通过多项式展开，可对算法的期望泛化误差进行分解（详细的推导参看[2]）：

\[
\begin{aligned}
\mathbb{E}_D[\left (f(x;D) - y_D \right)^2] & = \mathbb{E}_D[\left (f(x;D) - \bar{f}(x) + \bar{f}(x) - y_D \right)^2] \cr
& = \mathbb{E}_D[\left (f(x;D) - \bar{f}(x) \right)^2] + \left(\bar{f}(x) -y \right)^2 + \mathbb{E}_D[(y_D -y)^2] \cr
& = bias^2(x) + var(x) + \xi^2
\end{aligned}
\]

也就是说，误差可以分解为3个部分：bias、variance、noise。bias度量了算法本身的拟合能力，刻画模型的准确性；variance度量了数据扰动所造成的影响，刻画模型的稳定性。为了取得较好的泛化能力，则需要充分拟合数据（bias小），并受数据扰动的影响小（variance小）。但是，bias与variance往往是不可兼得的：

• 当训练不足时，拟合能力不够强，数据扰动不足以产生较大的影响，此时bias主导了泛化错误率；
• 随着训练加深时，拟合能力随之加强，数据扰动渐渐被学习到，variance主导了泛化错误率。

Bagging与Boosting

集成学习需要解决两个问题：

• 如何调整输入训练数据的概率分布及权值；
• 如何组合基分类器。

从上述问题的角度出发，集成学习分为两类流派：Bagging与Boosting。Bagging（Bootstrap Aggregating）对训练数据擦用自助采样（boostrap sampling），即有放回地采样数据；每一次的采样数据集训练出一个基分类器，经过\(M\)次采样得到\(M\)个基分类器，然后根据最大表决（majority vote）原则组合基分类器的分类结果。

Boosting的思路则是采用重赋权（re-weighting）法迭代地训练基分类器，即对每一轮的训练数据样本赋予一个权重，并且每一轮样本的权值分布依赖上一轮的分类结果；基分类器之间采用序列式的线性加权方式进行组合。

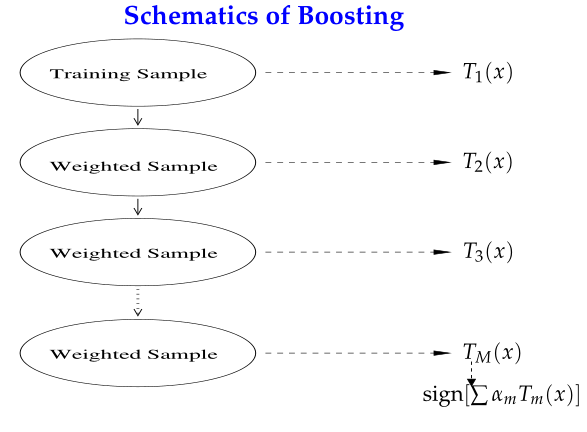
从“偏差-方差分解”的角度看，Bagging关注于降低variance，而Boosting则是降低bias；Boosting的基分类器是强相关的，并不能显著降低variance。Bagging与Boosting有分属于自己流派的两大杀器：Random Forests（RF）和Gradient Boosting Decision Tree（GBDT）。本文所要讲的AdaBoost属于Boosting流派。

2. AdaBoost算法

对于二分类问题，即\(y \in \lbrace 0,1 \rbrace\)；AdaBoost定义损失函数为指数损失函数：

\begin{equation}
L(y, f(x)) = exp(-yf(x)) \label{eq:loss}
\end{equation}

根据加型模型（additive model），第\(m\)轮的分类函数

\[
f_m(x) = f_{m-1}(x) + \alpha_mG_m(x)
\]

其中，\(\alpha_m\)为基分类器\(G_m(x)\)的组合系数。AdaBoost采用前向分布（forward stagewise）这种贪心算法最小化损失函数\eqref{eq:loss}，求解子模型的\(\alpha_m\)

\[
\alpha_m = \frac{1}{2}\log \frac{1-e_m}{e_m}
\]

其中，\(e_m\)为\(G_m(x)\)的分类误差率。第\(m+1\)轮的训练数据集权值分布\(D_{m+1} = (w_{m+1,1}, \cdots, w_{m+1,i}, \cdots, w_{m+1,N})\)

\[
w_{m+1,i} = \frac{w_{m,i}}{Z_m} exp(-\alpha_m y_i G_m(x_i))
\]

其中，\(Z_m\)为规范化因子

\[
Z_m = \sum_{i=1}^{N} w_{m,i} * exp(-\alpha_m y_i G_m(x_i))
\]

则得到最终分类器

\[
sign(f(x)) = sign\left( \sum_{m=1}^{M} \alpha_m G_m(x) \right)
\]

\(\alpha_m\)是\(e_m\)的单调递减函数，特别地，当\(e_m \leq \frac{1}{2}\)时，\(\alpha_m \geq 0\)；当\(e_m > \frac{1}{2}\)时，即基分类器不满足弱可学习的条件（比随机猜测好），则应该停止迭代。具体算法流程如下：

1 \(D_1(i) = 1/N\) % Initialize the weight distribution
2 for \(m = 1, \cdots, M\):
3 　　learn base classifier \(G_m(x)\);
4　　 if \(e_m > 0.5\) then break；
5　　update \(\alpha_m\) and \(D_{m+1}\);
6 end for

在算法第4步，学习过程有可能停止，导致学习不充分而泛化能力较差。因此，可采用“重采样”（re-sampling）避免训练过程过早停止；即抛弃当前不满足条件的基分类器，基于重新采样的数据训练分类器，从而获得学习“重启动”机会。

AdaBoost能够自适应（addaptive）地调整样本的权值分布，将分错的样本的权重设高、分对的样本的权重设低；所以被称为“Adaptive Boosting”。老师木在微博上提出了关于AdaBoost的三个问题：

1，adaboost不易过拟合的神话。2，adaboost人脸检测器好用的本质原因，3，真的要求每个弱分类器准确率不低于50%

3. 参考资料

[1] 李航，《统计学习方法》.
[2] 周志华，《机器学习》.
[3] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.
[4] Ji Zhu, Classification.
[5] 腾讯大数据，机器学习 刀光剑影 之屠龙刀.
[6] 过拟合, 为什么说bagging是减少variance，而boosting是减少bias?