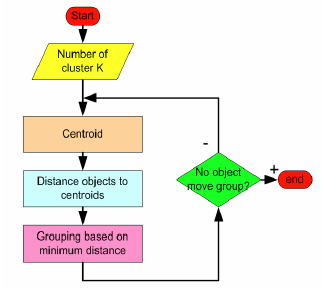
聚类:（K-means）算法

1.归类：

• 聚类(clustering) 属于非监督学习 (unsupervised learning)
• 无类别标记(class label)

2.举例：

3. K-means 算法：

 

     3.1 Clustering 中的经典算法，数据挖掘十大经典算法之一

     3.2 算法接受参数 k ；然后将事先输入的n个数据对象划分为 k个聚类以便使得所获得的聚类满足：同一

           聚类中的对象相似度较高；而不同聚类中的对象相似度较小。

     3.3 算法思想：

           以空间中k个点（可随机选取）为中心进行聚类，对最靠近他们的对象归类。通过迭代的方法，逐次更新各聚类中心     

           的值，直至得到最好的聚类结果

     3.4 算法描述：

          （1）适当选择c个类的初始中心；

          （2）在第k次迭代中，对任意一个样本，求其到c各中心的距离，将该样本归到距离最短的中心所在     

                  的类；

          （3）利用均值等方法更新该类的中心值；

          （4）对于所有的c个聚类中心，如果利用（2）（3）的迭代法更新后，值保持不变，则迭代结束，

                   否则继续迭代。

     3.5 算法流程：

输入：k, data[n];

          （1） 选择k个初始中心点，例如c[0]=data[0],…c[k-1]=data[k-1];

          （2） 对于data[0]….data[n], 分别与c[0]…c[k-1]比较，假定与c[i]差值最少，就标记为i;

          （3） 对于所有标记为i点，重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数；

          （4） 重复(2)(3),直到所有c[i]值的变化小于给定阈值。

 

4.举例： 

4.1 流程图：

4.2 一个药物分类的例子：

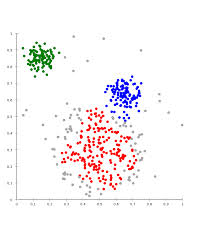
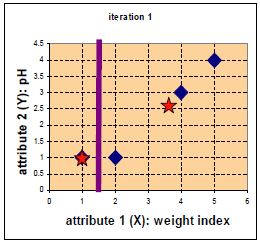
四中药物给予了 weight index 和 pH 两个特征。

在二维坐标系中的分布如下：

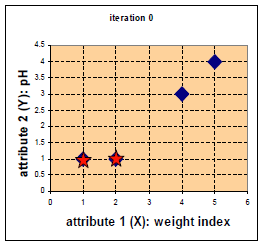
D0为第一次迭代，第一行为4个点到c1的距离，第二行为4个点到c2的距离。

　　　　

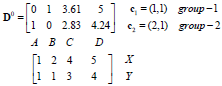
G0为第一次迭代后的归类情况，将各点到c1、c2的距离进行比较，哪个的距离小就为哪一类。

归类如下：c1为第一类，c2、c3、c4为第二类。

　　　　

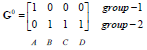
第二类的中心点更新如下：

　　　　

重新计算中心点如下（星为中心点）：（若该类中的点变化，则更新该类的中心点；否则不更新）

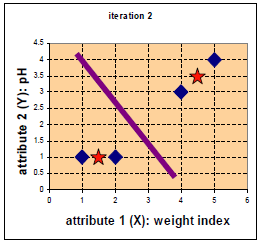
第二次迭代。

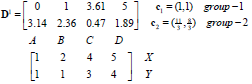
G1为第二次迭代后的归类情况。

归类如下：c1、c2为第一类，c3、c4为第二类。

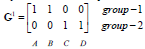
更新第一类、第二类的中心点如下：

　　

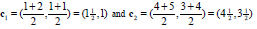
归类没有发生变化（达到终止条件）

　　

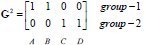
　　停止。

优点：速度快，简单

缺点：最终结果跟初始点选择相关，容易陷入局部最优，需直到k值