L1正则化及其推导

\(L1\)正则化及其推导

在机器学习的Loss函数中，通常会添加一些正则化（正则化与一些贝叶斯先验本质上是一致的，比如\(L2\)正则化与高斯先验是一致的、\(L1\)正则化与拉普拉斯先验是一致的等等，在这里就不展开讨论）来降低模型的结构风险，这样可以使降低模型复杂度、防止参数过大等。大部分的课本和博客都是直接给出了\(L1\)正则化的解释解或者几何说明来得到\(L1\)正则化会使参数稀疏化，本来会给出详细的推导。

\(L1\)正则化

大部分的正则化方法是在经验风险或者经验损失\(L_{emp}\)（emprirical loss）上加上一个结构化风险，我们的结构化风险用参数范数惩罚\(\Omega(\theta)\)，用来限制模型的学习能力、通过防止过拟合来提高泛化能力。所以总的损失函数（也叫目标函数）为：

\[
J(\theta; X, y) = L_{emp}(\theta; X, y) + \alpha\Omega(\theta) \tag{1.1}
\]

其中\(X\)是输入数据，\(y\)是标签，\(\theta\)是参数，\(\alpha \in [0,+\infty]\)是用来调整参数范数惩罚与经验损失的相对贡献的超参数，当\(\alpha = 0\)时表示没有正则化，\(\alpha\)越大对应该的正则化惩罚就越大。对于\(L1\)正则化，我们有：

\[
\Omega(\theta) = \|w\|_1 \tag{1.2}
\]

其中\(w\)是模型的参数。

几何解释

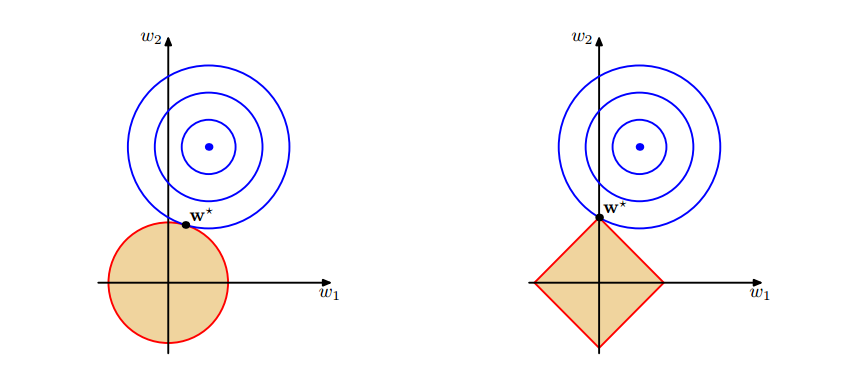
图1 上面中的蓝色轮廓线是没有正则化损失函数的等高线，中心的蓝色点为最优解，左图、右图分别为$L2$、$L1$正则化给出的限制。

可以看到在正则化的限制之下，\(L2\)正则化给出的最优解\(w^*\)是使解更加靠近原点，也就是说\(L2\)正则化能降低参数范数的总和。\(L1\)正则化给出的最优解\(w^*\)是使解更加靠近某些轴，而其它的轴则为0，所以\(L1\)正则化能使得到的参数稀疏化。

解析解的推导

有没有偏置的条件下，\(\theta\)就是\(w\)，结合式\((1.1)\)与\((1.2)\)，我们可以得到\(L1\)正则化的目标函数：

\[
J(w; X, y) = L_{emp}(w; X, y) + \alpha\|w\|_1 \tag{3.1}
\]

我们的目的是求得使目标函数取最小值的\(w^*\)，上式对\(w\)求导可得：

\[
\nabla_w J(w; X, y) = \nabla_w L_{emp}(w; X, y) + \alpha \cdot sign(w) \tag{3.2}
\]
其中若\(w>0\)，则\(sign(w)=1\)；若\(w<0\)，则\(sign(w) = -1\)；若\(w=0\)，则\(sign(w)=0\)。当\(\alpha = 0\)，假设我们得到最优的目标解是\(w^*\)，用秦勤公式在\(w^*\)处展开可以得到（要注意的\(\nabla J(w^*)=0\)）：

\[
J(w; X, y) = J(w^*; X, y) + \frac{1}{2}(w - w^*)H(w-w^*) \tag{3.3}
\]

其中\(H\)是关于\(w\)的Hessian矩阵，为了得到更直观的解，我们简化\(H\)，假设\(H\)这对角矩阵，则有：

\[
H = diag([H_{1,1},H_{2,2}...H_{n,n}]) \tag{3.4}
\]

将上式代入到式\((3.1)\)中可以得到，我们简化后的目标函数可以写成这样：

\[
J(w;X,y)=J(w^*;X,y)+\sum_i\left[\frac{1}{2}H_{i,i}(w_i-w_i^*)^2 + \alpha_i|w_i| \right] \tag{3.5}
\]

从上式可以看出，\(w\)各个方向的导数是不相关的，所以可以分别独立求导并使之为0，可得：

\[
H_{i,i}(w_i-w_i^*)+\alpha \cdot sign(w_i)=0 \tag{3.6}
\]

我们先直接给出上式的解，再来看推导过程：

\[
w_i = sign(w^*) \max\left\{ |w_i^*| - \frac{\alpha}{H_{i,i}},0 \right\} \tag{3.7}
\]

从式\((3.5)\)与式\((3.6)\)可以得到两点：

• 1.可以看到式\((3.5)\)中的二次函数是关于\(w^*\)对称的，所以若要使式\((3.5)\)最小，那么必有：\(|w_i|<|w^*|\)，因为在二次函数值不变的程序下，这样可以使得\(\alpha|w_i|\)更小。
• 2.\(sign(w_i)=sign(w_i^*)\)或\(w_1=0\)，因为在\(\alpha|w_i|\)不变的情况下，\(sign(w_i)=sign(w_i^*)\)或\(w_i=0\)可以使式\((3.5)\)更小。

由式\((3.6)\)与上述的第2点：\(sign(w_i)=sign(w_i^*)\)可以得到：

\[
\begin{split}
0 &= H_{i,i}(w_i-w_i^*)+\alpha \cdot sign(w_i^*) \cr
w_i &= w_i^* - \frac{\alpha}{H_{i,i}}sign(w_i^*) \cr
w_i &= sign(w_i^*)|w_i^*| - \frac{\alpha}{H_{i,i}}sign(w_i^*)\cr
&=sign(w_i^*)(|w_i^*| - \frac{\alpha}{H_{i,i}}) \cr
\end{split} \tag{3.8}
\]
我们再来看一下第2点：\(sign(w_i)=sign(w_i^*)\)或\(w_1=0\)，若\(|w_i^*| < \frac{\alpha}{H_{i,i}}\)，那么有\(sign(w_i) \neq sign(w_i^*)\)，所以这时有\(w_1=0\)，由于可以直接得到解式\((3.7)\)。
从这个解可以得到两个可能的结果：

• 1.若\(|w_i^*| \leq \frac{\alpha}{H_{i,i}}\)，正则化后目标中的\(w_i\)的最优解是\(w_i=0\)。因为这个方向上\(L_{emp}(w; X, y)\)的影响被正则化的抵消了。
• 2.若\(|w_i^*| > \frac{\alpha}{H_{i,i}}\)，正则化不会推最优解推向0，而是在这个方面上向原点移动了\(\frac{\alpha}{H_{i,i}}\)的距离。