[P1169] 棋盘制作 &悬线法学习笔记

学习笔记 悬线法

• 最大子矩阵问题：

在一个给定的矩形中有一些障碍点，找出内部不包含障碍点的，边与整个矩形平行或重合的最大子矩形。

极大子矩型：无法再向外拓展的有效子矩形

最大子矩型：最大的一个有效子矩形

特别的，在一个有障碍点的矩形中，最大子矩形一定是极大子矩形

• 悬线法

悬线：上端覆盖了一个障碍点或者到达整个矩形上边界的有效线段

每个悬线上的点的与底部的点一一对应，矩形中每一个点（矩形顶部点除外）都对应了一条悬线。

如果把一条悬线向左右两个方向尽可能的移动，那么就得到了一个矩形。

注意：悬线对应的矩型不一定是极大子矩阵，因为悬线定义中固定了悬线的下边界，故而，悬线左右移动所得到的矩形无法向下扩展。

• 悬线法的实现

      三个重要的元素：

1. height_i,j ：表示以( i ,j )为底的悬线的高 (初始化为1)
2. left_{i,j        ：表示向左最多能移动到的位置  （初始化为j）}
3. right_{i,j     ： 表示向右最多能移动到的位置   （初始化为j）}

其中的left,right要视题目要求进行进一步的初始化，如例题

转移：

如果点  不是障碍点，那么，以  为底的悬线就等于以  为底的悬线加点  到点       的线段。因此，  。

当然还要注意左右边界的问题

以上图片转自  https://zhuanlan.zhihu.com/p/46382722

画个图理解一下

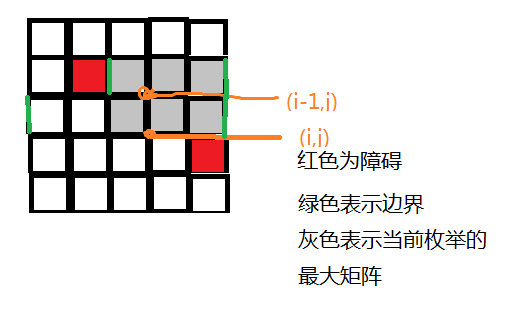
那么计算面积就轻而易举

对于以点  为底的悬线对应的子矩形，其面积计算为

问题解：

时间复杂度：  ；空间复杂度： 

例题：luogu P1169 棋盘制作

直接上代码

 #include<cstdio>
 #include<algorithm>
 #include<iostream>
 #define maxn 2010
 #define re register
 using namespace std;
 int n,m,ans1,ans2;
 int map[maxn][maxn],height[maxn][maxn];
 int l[maxn][maxn],r[maxn][maxn];
 int main()
 {
     scanf("%d%d",&n,&m);
     for(re int i=;i<=n;++i)
      for(re int j=;j<=m;++j)
      {
          scanf("%d",&map[i][j]);
          height[i][j]=;
          l[i][j]=r[i][j]=j;
      }
     for(re int i=;i<=n;++i)
      for(re int j=;j<=m;++j)
      {
          if(map[i][j]!=map[i][j-])
          l[i][j]=l[i][j-];
      }
     for(re int i=;i<=n;++i)
      for(re int j=m-;j>=;j--)
      {
          if(map[i][j]!=map[i][j+])
          r[i][j]=r[i][j+];
      }
     //以上为初始化
     for(re int i=;i<=n;++i)
       for(re int j=;j<=m;++j)
       {
           if(i>&&map[i][j]!=map[i-][j])
           {
               height[i][j]=height[i-][j]+;
               l[i][j]=max(l[i][j],l[i-][j]);
               r[i][j]=min(r[i][j],r[i-][j]);
         }
         int a=r[i][j]-l[i][j]+;
         int b=min(height[i][j],a);
         ans1=max(ans1,a*height[i][j]);//最大矩形
         ans2=max(ans2,b*b);//最大正方形
       }
       printf("%d\n%d",ans2,ans1);
     return ;
 }

注：部分内容转载自  
Flavius Buffon：悬线法用来求解最大子矩形问题 同时也是参考文献