基于C++的牛顿切线法演示

牛顿切线法

---

中心思想：

　　利用目标函数二阶泰勒多项式的最优解作为函数的近似最优解。如果新的近似最优解满足计算精度，则终止计算，否则将函数在新点展开成二阶泰勒多项式，用新的泰勒多项式的最优解作为函数的近似最优解，如此迭代，直到倒数为零或者其绝对值小于事先给定的精度 e 为止。

计算过程：

　　设函数 f(x) 在区间 [a,b] 上是严格下凸的，即二阶导数 f ^''(x) > 0 ，并且存在点 x*∈(a,b) 使得 f^'(x*)=0 。此时必有 f^'(a)·f^'(b) < 0，任取x₀∈[a,b],将 f(x) 在 x₀ 处展开，有：

令：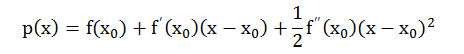

则：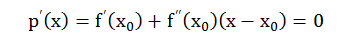

则 f(x)≈p(x) ，p(x) 是二次函数，其最小值点位于: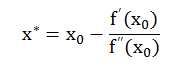

用 p(x) 的最小值点作为 f(x) 的最小值点 x₁ 的近似值，然后再利用 f(x) 在 x₁ 处的泰勒展开式的二次多项式的最小值点作为 f(x) 的近似值点 x₂ ，如此迭代下去，得:

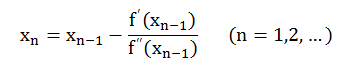于是，当 x_n 收敛时，设

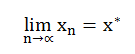
则有：

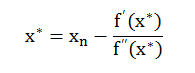
即 f^'(x*)=0 ，从而得到 f(x) 的最小值点 x* 。

在例题中实现C++程序设计：

例：编写牛顿切线法的计算程序计算函数 f(x)=2x³-12x+9 在区间 [-1,3] 上的最小值，精度取0.001。

在 Dev 编译器中 C++ 代码如下：

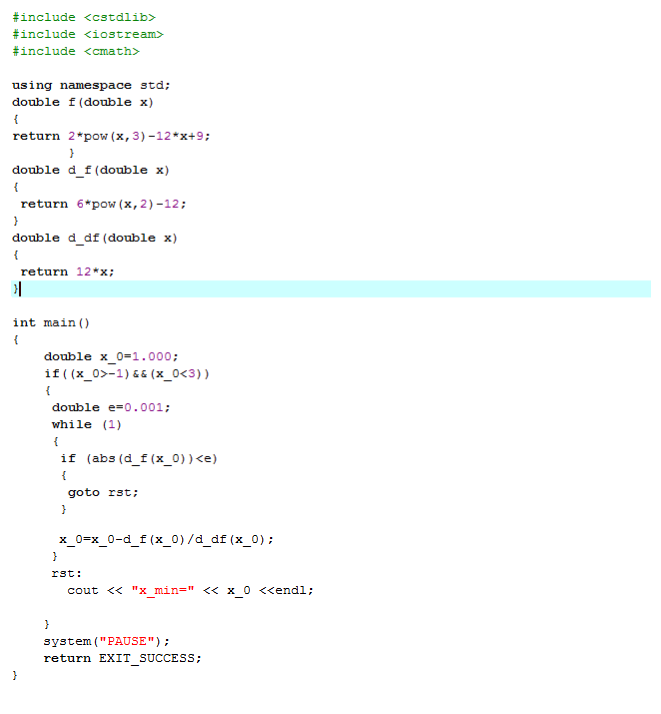
运行程序结果如下：

由于作者水平有限，文中不当之处还望看到的朋友指出，谢谢！