Cesium中用到的图形技术——Computing the horizon occlusion point

译者注：本文翻译自Cesium官方博文《Computing the horizon occlusion point》，by KEVIN RING。

你厌倦了地平线剔除吗？ 太好了，我也没有！

上一次，我们解释了地平线剔除是关于什么的，并展示了一种非常有效的方法来测试一个点是否被椭圆体遮挡。然而，我们想要测试遮挡的对象很少是简单的点。特别是，我们希望能够测试地形瓦片是否被椭球体遮挡。但是地形瓦片是由数千个顶点组成的复杂对象。

Deron Ohlarik在上一篇博客文章中谈到了此问题，他解释说，对于任何任意几何图形，我们都可以计算与几何图形有特殊关系的点的位置（我们称为水平遮挡点）。无论观察者从哪个方向接近几何体，该点都会同时或在几何体的任何部分变为可见之前对观察者可见。这正是我们所需要的！但是，如何计算这样的点的许多细节留给读者练习。此外，还不清楚这种方法是否可以推广到椭球而不是球体。该博客旨在填补这两个空白。

再次，这里介绍的技术完全归功于Frank Stoner。

让我们来看看我们的情况。和以前一样，我们通过将每个分量 X、Y和Z乘以沿该轴的椭球半径的倒数，将所有坐标转换到椭球尺度空间。

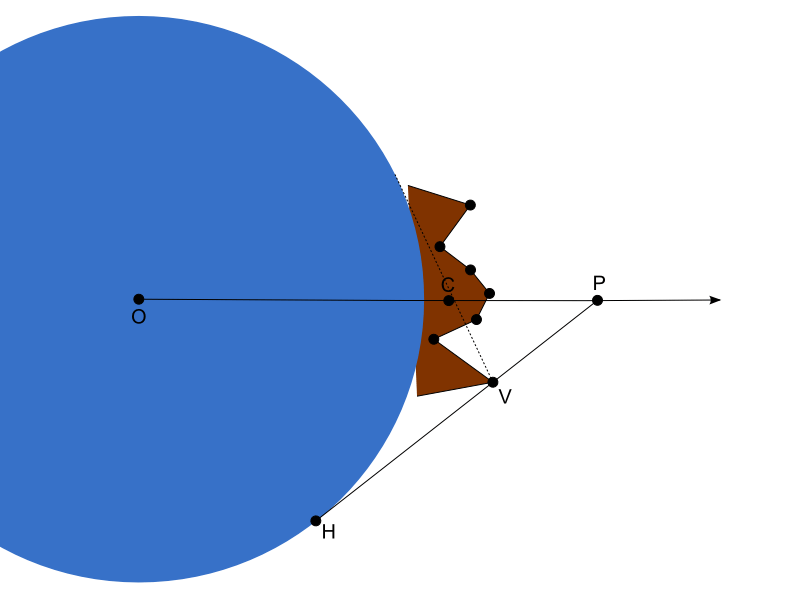
在此图中，地球以蓝色显示，地形图块以棕色显示。在尺度空间中，地球是一个单位球体。围绕地形图块的边界球的中心显示为点C。边界球不是缩放空间中的球体，但这与我们无关，因为我们将只使用它的中心。

首先，我们任意决定我们的地平线遮挡点将位于这条中心线OC的某个位置，OC是从地球中心到地形图块边界球中心的向量。我们只需要计算它沿该向量的距离。点V是地形图块中的一个顶点。点H是从V的角度看地平线上的一个点。从V的角度看，有无数个地平线点，在单位球面上形成一个圆，但这些地平线点中只有两个点通过V形成一个向量，或与中心线相交。一个显示为实线HP。另一个显示为连接到V为虚线。在虚线上，与中心线的交点出现在点V之前，所以它会比另一个交点更靠近椭球的中心，我们不需要关心它。如果点V是地形图块中的唯一顶点，那么此图中的点P将是我们的地平线遮挡点。对于多个顶点，我们对每个顶点重复 P 的计算，然后选择离椭圆体最远的那个。

那么我们如何计算给定地形瓦片顶点的P点呢？让我们标记下图中的各个角度。

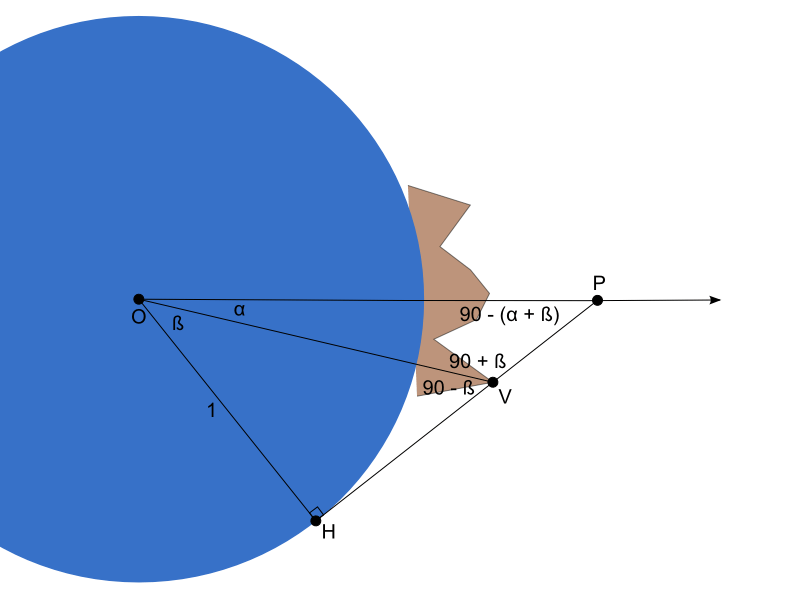
在标记角α和β之后，通过简单的三角形角的知识，我们可以通过他们表达其他的角。

接下来，根据正弦定律：

\[\frac{\lVert \vec{OP} \rVert }{sin(90+β)} = \frac{\lVert \vec{OV} \rVert}{sin(90-(α+β))}
\]

根据三角函数\(sin(90+θ) = cos(θ)\)，有：

\[\frac{\lVert \vec{OP} \rVert }{cos(β)} = \frac{\lVert \vec{OV} \rVert}{cos(α+β)}
\]

\[\lVert \vec{OP} \rVert = \frac{\lVert \vec{OV} \rVert cos(β)}{cos(α+β)}
\]

β是直角三角形中的角，因此有：

\[cos(β) = \frac{\lVert \vec{OH} \rVert}{\lVert \vec{OV} \rVert} = \frac{1}{\lVert \vec{OV} \rVert}
\]

\[\lVert \vec{OP} \rVert = \frac{\lVert \vec{OV} \rVert \frac{1}{\lVert \vec{OV} \rVert}}{cos(α+β)}
\]

\[\lVert \vec{OP} \rVert = \frac{1}{cos(α+β)}
\]

然后，我们使用复合角公式：

\[cos(α+β) = cos(α)cos(β) - sin(α)sin(β)
\]

\[\lVert \vec{OP} \rVert = \frac{1}{cos(α)cos(β) - sin(α)sin(β)}
\]

我们已经知道如何去计算\(cos(β)\)。同样通过勾股定理，我们能计算\(sin(β)\)：

\[sin(β) = \frac{\lVert \vec{HV} \rVert}{\lVert \vec{OV} \rVert}
\]

\[\lVert \vec{HV} \rVert = \sqrt{\lVert \vec{OV} \rVert^2-\lVert \vec{OH} \rVert^2} = \sqrt{\lVert \vec{OV} \rVert^2-1}
\]

\[sin(β) = \frac{\sqrt{\lVert \vec{OV} \rVert^2-1}}{\lVert \vec{OV} \rVert}
\]

通过点积的定义，我们能够计算\(cos(α)\)：

\[\vec{OV} \cdot \hat{OP} = \lVert \vec{OV} \rVert cos(α)
\]

\[cos(α) = \frac { \vec{OV} \cdot \hat{OP} } {\lVert \vec{OV} \rVert}
\]

\[cos(α) = \hat{OV} \cdot \hat{OP}
\]

最后，通过矢量叉积的模，我们能够计算\(sin(α)\)：

\[\lVert \hat{OP} \times \vec{OV} \rVert = \lVert \vec{OV} \rVert sin(α)
\]

\[sin(α) = \lVert \hat{OP} \times \hat{OV} \rVert
\]

通过以上的计算，我们就能够计算\(OP\)的模了。汇总如下：

\[cos(β) = \frac{1}{\lVert \vec{OV} \rVert}
\]

\[sin(β) = \frac{\sqrt{\lVert \vec{OV} \rVert^2-1}}{\lVert \vec{OV} \rVert}
\]

\[cos(α) = \hat{OV} \cdot \hat{OP}
\]

\[sin(α) = \lVert \hat{OP} \times \hat{OV} \rVert
\]

\[\lVert \vec{OP} \rVert = \frac{1}{cos(α)cos(β) - sin(α)sin(β)}
\]

请记住，我们通过构造了解\(\hat{OP}\)；我们选择它从椭圆体的中心指向地形图块的边界球体的中心。为了计算点P在椭球尺度空间中的位置，我们简单地将方向乘以上面计算的模。由于我们的遮挡测试使用缩放空间中表示的点，因此我们完成了。如果我们还想知道真实、未密封坐标中的位置，我们只需要将位置的每个分量乘以沿相应轴的椭球半径。

下面是 Cesium 中的代码，为了清晰起见略作调整：

function computeMagnitude(ellipsoid, position, scaledSpaceDirectionToPoint) {
    var scaledSpacePosition = ellipsoid.transformPositionToScaledSpace(position);
    var magnitudeSquared = scaledSpacePosition.magnitudeSquared();
    var magnitude = Math.sqrt(magnitudeSquared);
    var direction = scaledSpacePosition.divideByScalar(magnitude);

    // For the purpose of this computation, points below the ellipsoid
    // are considered to be on it instead.
    magnitudeSquared = Math.max(1.0, magnitudeSquared);
    magnitude = Math.max(1.0, magnitude);

    var cosAlpha = direction.dot(scaledSpaceDirectionToPoint);
    var sinAlpha = direction.cross(scaledSpaceDirectionToPoint).magnitude();
    var cosBeta = 1.0 / magnitude;
    var sinBeta = Math.sqrt(magnitudeSquared - 1.0) * cosBeta;

    return 1.0 / (cosAlpha * cosBeta - sinAlpha * sinBeta);
}

如您所见，此计算比我们上次描述的用于在地平线上测试该点的计算成本更高。可能可以通过使用前面描述的锥体测试测试每个顶点来优化它，并且如果发现顶点在锥体之外，则仅计算顶点的精确水平遮挡点。我将把它留给读者作为练习。

无论如何，这种计算的成本是它主要只适用于静态几何的主要原因。如果几何体相对于椭球体发生变化，则需要在每次变化时重复此计算。这可能会变得昂贵。

另外，在使用这种方法时，请记住一个重要的警告。在现实世界中，被WGS84椭球遮挡的物体不一定被地球的真实表面遮挡。这是因为地球表面实际上在世界部分地区略低于椭球体。根据您的应用，使用WGS84作为遮挡体积可能是可以接受的，或者您可能需要使用更保守的椭球。