【LeetCode】062. Unique Paths

题目：

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

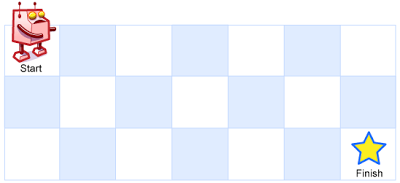
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

题解：

Solution 1 ()

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m< || n<) return ;
        if(m == && n == ) return ;
        vector<vector<int>> dp(m, vector<int> (n,));
        for(int i=; i<m; ++i) {
            for(int j=; j<n; ++j) {
                dp[i][j] = dp[i-][j] + dp[i][j-];
            }
        }
        return dp[m-][n-];
    }
};

　　用一维数组存储，d[j] = d[j] + d[j-1];这里的等号右边d[j]相当于d[i-1][j]，d[j-1]相当于d[i][j-1];

Solution 2 ()

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> dp(n, );
        for (int i = ; i < m; ++i) {
            for (int j = ; j < n; ++j) {
                dp[j] += dp[j - ];
            }
        }
        return dp[n - ];
    }
};　

First of all you should understand that we need to do n + m - 2 movements : m - 1 down, n - 1 right, because we start from cell (1, 1).

Secondly, the path it is the sequence of movements( go down / go right),
therefore we can say that two paths are different
when there is i-th (1 .. m + n - 2) movement in path1 differ i-th movement in path2.

So, how we can build paths.
Let's choose (n - 1) movements(number of steps to the right) from (m + n - 2),
and rest (m - 1) is (number of steps down).

I think now it is obvious that count of different paths are all combinations (n - 1) movements from (m + n-2). (from here)

Solution 3 ()

class Solution {
public:
    int uniquePaths(int m, int n) {
        int N = n + m - ;// how much steps we need to do
        int k = m - ; // number of steps that need to go down
        double res = ;
        // here we calculate the total possible path number
        // Combination(N, k) = n! / (k!(n - k)!)
        // reduce the numerator and denominator and get
        // C = ( (n - k + 1) * (n - k + 2) * ... * n ) / k!
        for (int i = ; i <= k; i++)
            res = res * (N - k + i) / i;
        return (int)res;
   }
};