栈(stack)、递归（八皇后问题）、排序算法分类，时间和空间复杂度简介

一、栈的介绍：

1)栈的英文为(stack)
2)栈是一个先入后出(FILO-First In Last Out)的有序列表。
3)栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一
种特殊线性表。允许插入和删除的一端，为变化的一端，称为栈顶(Top)，另一端为固定的一端，称为栈底(Bottom)。
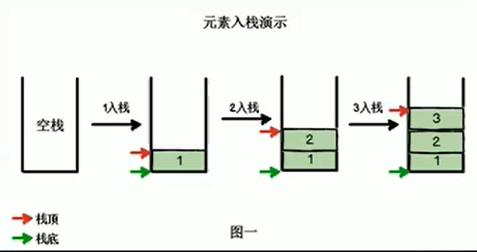
4)根据栈的定义可知，最先放入栈中元素在栈底，最后放入的元素在栈顶，而
删除元素刚好相反，最后放入的元素最先删除，最先放入的元素最后删除

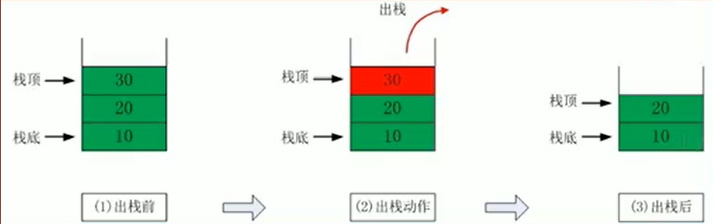
5）出栈（pop）和入栈（push）的概念

栈的使用场景：

1)子程序的调用:在跳往子程序前，会先将下个指令的地址存到堆栈中，直到
子程序执行完后再将地址取出，以回到原来的程序中。1
2)处理递归调用:和子程序的调用类似，只是除了储存下一个指令的地址外，
也将参数、区域变量等数据存入堆栈中。
3)表达式的转换【中缀表达式转后缀表达式】与求值(实际解决)。
4)二叉树的遍历。
5)图形的深度优先(depth一first)搜索法。

使用栈实现一个简单的计算机功能：

import java.util.Stack;

public class Calculator {
    public static void main(String[] args) {
        //获取一个和栈相关计算操作的对象
        AboutStack stack = new AboutStack();
        String calcu = "2000*1+3*2-4";
        //将字符串转换为一个char数组
        char[] chars = calcu.toCharArray();

        //循环数组，判断字符为数字还是操作符，进行添加和计算
        for (char ch:chars) {
            if ('0' <= ch && ch <= '9') {
                //添加数字到数字栈中
                stack.addToNumStack(ch);
            }else {
                //添加符号到符号栈中
                stack.addToSymbolStack(ch);
            }
        }
        //进行最后结果的计算和输出
        System.out.println(stack.calculator(stack.numStack.pop(),stack.numStack.pop(),stack.symbolsStack.pop()));

    }

}
class AboutStack{
    public Stack<Integer> numStack;
    public Stack<Character> symbolsStack;
    public boolean next = false;

    public AboutStack() {
        //初始化数字栈和字符栈
        numStack = new Stack<>();
        symbolsStack = new Stack<>();
    }
    //添加数到数值栈中
    public void addToNumStack(char ch){
        if (numStack.isEmpty()) {//判断当前栈是否为空，如果为空就直接将数字加入到数字栈中
            numStack.push(Integer.parseInt(String.valueOf(ch)));
            next = true;
            return;
        }
        if (next ){//判断是否连续的两个char字符都是数字，如果是，就表示是多位的数字，得到多位数字再放入到栈中
            int num = numStack.pop();
            String temp = num +""+String.valueOf(ch);//将上一个字符和现在的字符拼接成一个字符串，再将字符串转换为数字存放在数值栈中
            numStack.push(Integer.parseInt(temp));
            next = true;
        }else {
            //表示上一个存放的是字符，所以这次的数字直接放入到数字栈中
            numStack.push(Integer.parseInt(String.valueOf(ch)));
            next = true;
        }
    }
    //添加符号到符号栈中
    public void  addToSymbolStack(char ch){
        //如果符号栈为空，直接将符号放入到栈中
        if (symbolsStack.isEmpty()) {
            symbolsStack.push(ch);
            next = false;
            return;
        }
        //如果该符号的优先级小于或者等于上一个符号，就先计算上一个符号优先级较大的，、
        // 再将计算结果放入到数值栈，将该符号放入到栈中
        if (priority(ch) <= priority(symbolsStack.peek())) {
            numStack.push(calculator(numStack.pop(), numStack.pop(), symbolsStack.pop()));
            addToSymbolStack(ch);
            //            symbolsStack.push(ch);
            next = false;
        }else{
            symbolsStack.push(ch);
            next = false;
        }

    }
    //判断符号的优先级
    public int priority(char oper){
        if (oper == '*' || oper == '/') {
            return 2;
        }
        if (oper == '+' || oper == '-') {
            return 1;
        }else {
            return -1;
        }
    }

    //根据数值和符号计算出两个数的值
    public int calculator(int num1,int num2,char ch){
        int res = 0; // res 用于存放计算的结果
        switch (ch) {
            case '+':
                res = num1 + num2;
                break;
            case '-':
                res = num2 - num1;// 注意顺序
                break;
            case '*':
                res = num1 * num2;
                break;
            case '/':
                res = num2 / num1;
                break;
            default:
                break;
        }
        return res;
    }

}

二、前缀（波兰表达式）、中缀、后缀表达式（逆波兰表达式）

 前缀表达式的计算机求值：

中缀表达式：

后缀表达式（逆波兰表达式）：

三、递归：就是方法自己调用自己，每次调用时传入不同参数

1、递归调用机制的讲解

（1）当程序执行到一个方法时，就会开辟一个独立的空间（栈）

（2）每个空间的数据（局部变量），是独立的，不会相互影响

（3）如果方法中的使用的引用类型变量（比如数组），就会共享该引用类型的数据。

（4）递归必须向退出递归的条件逼近，否则就是无线递归，出现Stack OverflowError，死龟（归）了；

（5）当一个方法执行完毕，或者遇到return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或者返回时，该方法也就执行完毕。

2、递归常用的场景

1)各种数学问题如:8皇后问题﹐汉诺塔，阶乘问题,迷宫问题,球和篮子的问题(google编程大赛)

2)各种算法中也会使用到递归，比如快排，归并排序，二分查找，分治算法等.
3)将用栈解决的问题-->第归代码比较简洁

特别：八皇后问题（在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法..（92种）.）

package com.zjl.recursion;

public class Recursion {
    public static void main(String[] args) {

        Queen8 queen8 = new Queen8();
        queen8.Check(0);
        System.out.println("符合八皇后的位置个数一共有："+queen8.count);
    }
}

class Queen8 {
    //定义所有坐标的长度，表示一共8个皇后
    private static final int max = 8;
    //确定一个数组，表示8个皇后在每行的第几个位置
    private int[] arr = new int[max];
    //统计一共有多少个解
    public static int count = 0;

    public void Check(int n) {
        //判断是否到达最后一个皇后，如果是就将该数组输出
        if (n >= max) {
            Print();
            return;
        }
        //如果不是，就将该皇后从该列的的第一个位置开始放，直到找到适合它的位置
        for (int i = 0; i < max; i++) {
                arr[n] = i;//将该皇后放在该列上
            if (Judge(n)) {//判断该皇后的位置是否正确，如果返回结果是正确的，那就继续放下一个皇后
                Check(n + 1);
            }
        }
    }

    //判断该皇后放置的位置是否满足八皇后的要求
    public boolean Judge(int n) {
        /**
         * 1、arr[i] == arr[n]判断该皇后的位置是否和她前面的皇后的位置是在同一列，在就返回false
         * 2、Math.abs(i - n) == Math.abs(arr[i] - arr[n])判断该皇后的对角线上（斜线）有没有皇后，有就返回false
         * 3、如果返回结果为true就表示该位置可以放该皇后，不用判断不同皇后是否在同一行
         * 因为每一行都只安排了一个皇后放置
         */
        for (int i = 0; i < n; i++) {
            if (arr[i] == arr[n] || Math.abs(i - n) == Math.abs(arr[i] - arr[n])) {
                return false;
            }
        }
        return true;
    }

    //输出一个完整的可以完成8皇后的数组
    public void Print() {
        count++;//进行输出操作，说明就有一个数组满足8皇后的要求，对统计的和加一
        for (int i = 0; i < max; i++) {
            System.out.printf("%d ", arr[i]);
        }
        System.out.println();//每一个数组输出后都进行换行操作
    }

}

四、排序算法

1、排序也称排序算法
(Sort Algorithm)，排序是将一组数据，依指定的顺序进行排列的过程。
排序的分类:

1)内部排序:
指将需要处理的所有数据都加载到内部存储器中进行排序。
2)外部排序法:
数据量过大，无法全部加载到内存中，需要借助外部存储进行排序。

3）常见的排序算法

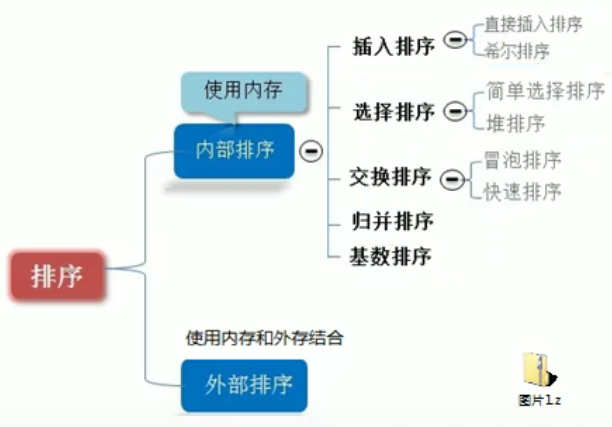
2、算法的时间复杂度（度量一个程序算法执行时间的两种方法）

1)事后统计的方法
这种方法可行,但是有两个问题:一是要想对设计的算法的运行性能进行评测，需要实际运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素,这种方式，要在同一台计算机的相同状态下运行，才能比较那个算法速度更快。
2)事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优.

时间频度：

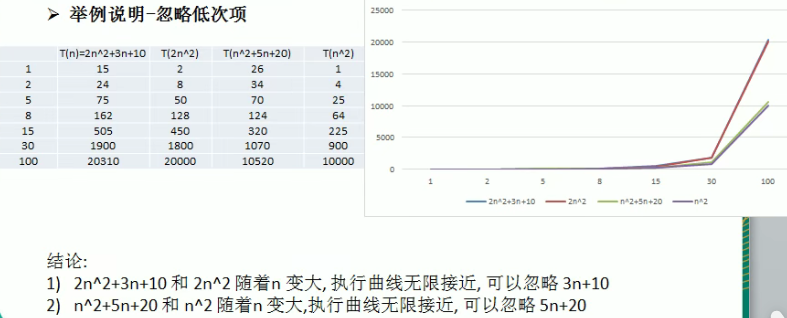
基本介绍：时间频度:一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

时间复杂度说明;

1)一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函
数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/ f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=o( f(n))，称O( f(n)）为算法的渐进时间复杂度，简称时间复杂度。
2) T(n)不同，但时间复杂度可能相同。如: T(n)=n2+7nt6与T(n)=3n2+2n+2它
们的T(n)不同，但时间复杂度相同，都为O(n2)。
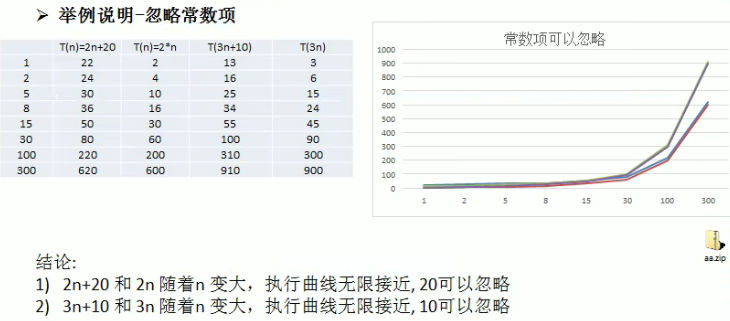
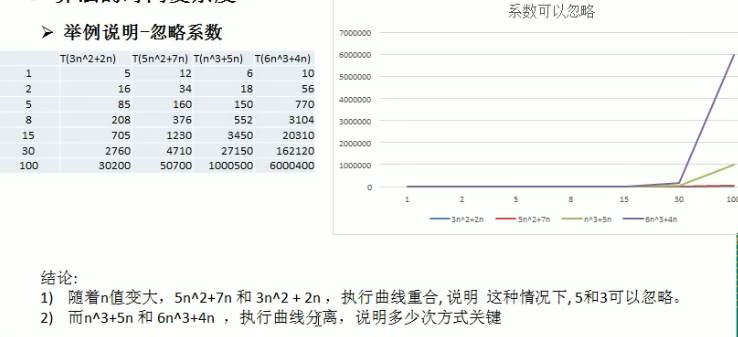
3)计算时间复杂度的方法:
(1)用常数1代替运行时间中的所有加法常数

(2)修改后的运行次数函数中，只保留最高阶项

(3)去除最高阶项的系数

常见的时间复杂度:实际应用中应该尽可能避免使用指数阶的算法

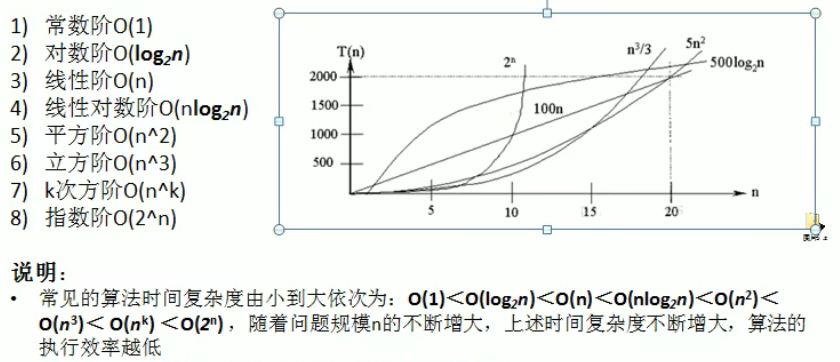
（1）常数阶O(1)

（2）对数阶O(log_2ⁿ):其中2可以是任意的整数

（3）线性阶O(n)

（4）线性对数阶O(nlog^N)

(5)平方阶O(n^₂)

（6）立方阶O(n³)、K次方阶O(n^k):相当于上面的n次循环

平均时间复杂度和最坏时间复杂度

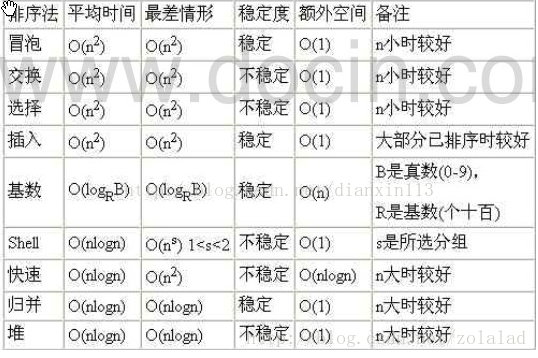
算法的空间复杂度：

基本介绍：

1)）类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该
算法所耗费的存储空间，它也是问题规模n的函数。
2)空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大
小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况
3)在做算法分析时，主要讨论的是时间复杂度。从用户使用体验上看，更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用
空间换时间.