CSU 1804 - 有向无环图 - [(类似于)树形DP]

题目链接：http://acm.csu.edu.cn/csuoj/problemset/problem?pid=1804

Bobo 有一个 n 个点，m 条边的有向无环图（即对于任意点 v，不存在从点 v 开始、点 v 结束的路径）。

为了方便，点用 1,2,…,n 编号。 设 count(x,y) 表示点 x 到点 y 不同的路径数量（规定 count(x,x)=0），Bobo 想知道

 

 

除以 (10 ⁹+7) 的余数。

其中，a _i,b _j 是给定的数列。

 

Input

输入包含不超过 15 组数据。

每组数据的第一行包含两个整数 n,m (1≤n,m≤10 ⁵).

接下来 n 行的第 i 行包含两个整数 a _i,b _i (0≤a _i,b _i≤10 ⁹).

最后 m 行的第 i 行包含两个整数 u _i,v _i，代表一条从点 u _i 到 v _i 的边 (1≤u _i,v_i≤n)。

 

Output对于每组数据，输出一个整数表示要求的值。Sample Input

3 3
1 1
1 1
1 1
1 2
1 3
2 3
2 2
1 0
0 2
1 2
1 2
2 1
500000000 0
0 500000000
1 2

Sample Output

4
4
250000014

题解：

首先，假如我们计算$\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times a_i \times b_j } \right)} } $

这个的时候，固定一个点i，枚举j进行计算的话，就有：

$a_i \times \left[ {\sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times b_j } \right)} } \right]$

我们不妨设$dp\left[ i \right] = \sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times b_j } \right)} $

那么，最后的${\rm{ans}} = \sum\limits_{i = 1}^n {\left\{ {a_i \times \left[ {\sum\limits_{j = 1}^n {\left( {count\left( {i,j} \right) \times b_j } \right)} } \right]} \right\}} $

问题来了，状态转移方程是什么？

假设对于点i，它有K个子节点，就有：

$dp\left[ i \right] = \sum\limits_{k = 1}^K {\left( {b_k + dp\left[ k \right]} \right)} $

（根据题意无环图，则存在 Edge(i→k) 就一定不存在一条路径从k点到i点，所以计算dp[k]时就一定不会涉及到dp[i]）

另外，本题如果不是有向无环图而是一棵树的话，很显然，直接从树根往下dfs计算每个节点i的dp[i]即可，

但是现在有向无环图，可能出现如下情况：

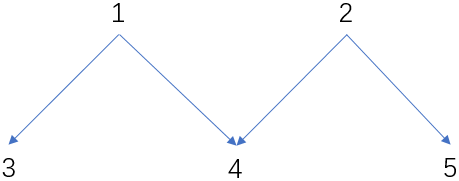
这样一来，如果主函数里单单dfs(1)或者单单dfs(2)都不能把整个图上所有节点的dp[i]都计算到，

因此要把所有in-degree[i]==0的节点i都dfs(i).

AC代码：

#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
typedef long long LL;

const LL MOD=1e9+;
const int maxn=1e5+;

int n,m;
int indegree[maxn];
LL a[maxn],b[maxn];
LL dp[maxn];

struct Edge{
    int u,v;
    Edge(int u,int v){this->u=u,this->v=v;}
};
vector<Edge> E;
vector<int> G[maxn];
void init(int l,int r)
{
    E.clear();
    for(int i=l;i<=r;i++) G[i].clear();
}
void addedge(int u,int v)
{
    E.push_back(Edge(u,v));
    G[u].push_back(E.size()-);
}

LL dfs(int u)
{
    if(dp[u]!=-) return dp[u];

    dp[u]=;
    for(int i=,_size=G[u].size();i<_size;i++)
    {
        Edge &e=E[G[u][i]]; int v=e.v;
        dp[u]=(dp[u]+b[v]+dfs(v))%MOD;
    }
    return dp[u];
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        for(int i=;i<=n;i++) scanf("%d%d",&a[i],&b[i]);

        init(,n); //邻接表初始化
        memset(indegree,,sizeof(indegree));
        for(int i=,u,v;i<=m;i++)
        {
            scanf("%d%d",&u,&v);
            addedge(u,v);
            indegree[v]++;
        }

        memset(dp,-,sizeof(dp));
        for(int i=;i<=n;i++)
        {
            if(indegree[i]==) dfs(i);
        }

        LL ans=;
        for(int i=;i<=n;i++) ans = ( ans + (dp[i]*a[i]) % MOD ) % MOD;

        printf("%lld\n",ans);
    }
}