Dijkstra求最短路 I（朴素算法）

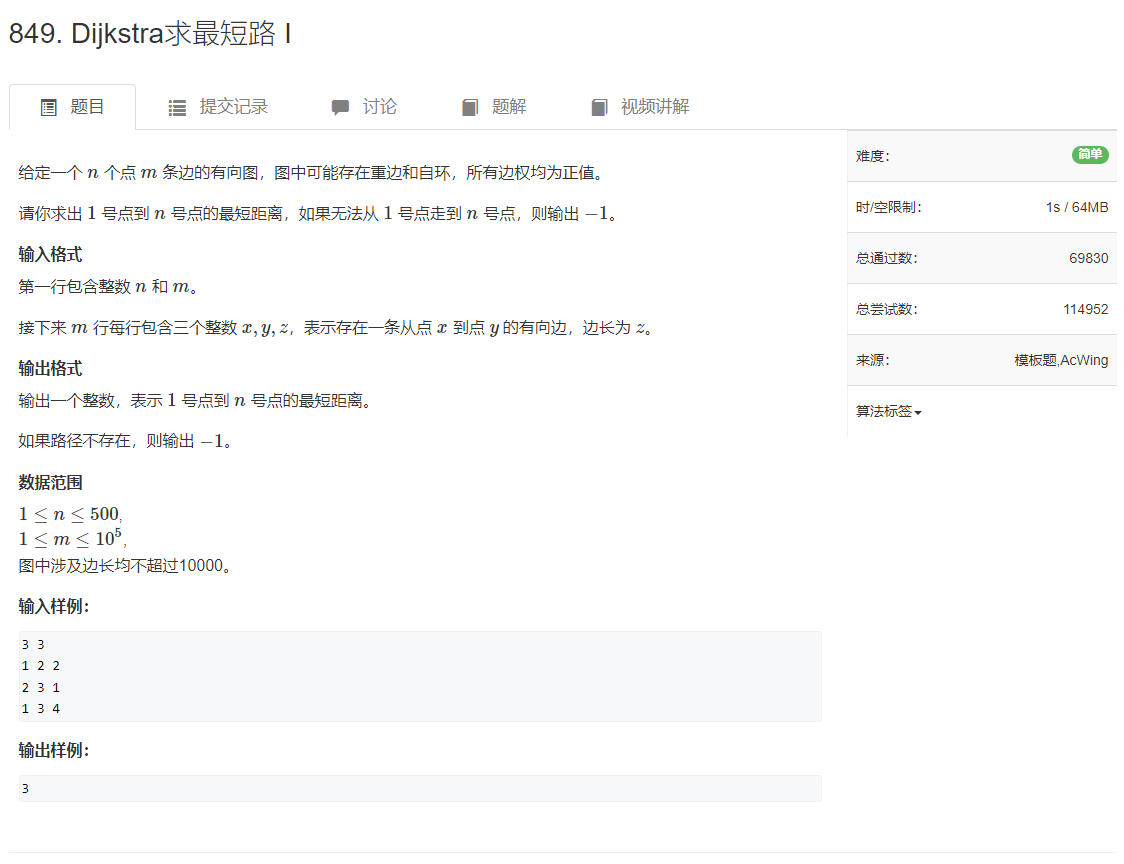
这道题目又是一个新算法，名叫Dijkstra

主要思路是：输入+dist和vis初始化（都初始化为0x3f）+输入g（邻接矩阵）+Dijkstra函数       Dijkstra函数：先将dist[1]设为1（起点到起点当然0代价），然后将每个点都更新一遍。在循环里面我们先找出最小但没更行新的点然后用这个点更新一遍所有数。在最后我们判断一下结束点的dist值如果等于0x3f说明结束点没被更行过一次，也就说明到不了结束点就返回-1，否则返回结束点的dist值即可。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int g[N][N],n,m,dist[N];
bool st[N];
int d()
{
    dist[1]=0;
    for (int i = 0; i < n; i ++ )
    {
        int t=-1;
        for (int j = 1; j <= n; j ++ )
        {
            if(!st[j]&&(t==-1||dist[t]>dist[j]))
            {
                t=j;
            }
        }
        st[t]=true;
        for (int j = 1; j <= n; j ++ )
        {
            dist[j]=min(dist[j],dist[t]+g[t][j]);
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    else return dist[n];
}
int main()
{
    scanf("%d%d", &n, &m);
    memset(dist,0x3f,sizeof dist);
    memset(g,0x3f,sizeof g);
    while (m -- )
    {
        int x,y,z;
        scanf("%d%d%d", &x, &y,&z);
        g[x][y]=min(g[x][y],z);
    }
    cout<<d();
    return 0;
}