OpenCASCADE 3 Planes Intersection

OpenCASCADE 3 Planes Intersection

eryar@163.com

Abstract. OpenCASCADE provides the algorithm to search the intersection point between 3 planes. If two of the planes are parallel or identical, will get no result.

Key Words. Plane Intersection

1.Introduction

由《高等数学》可知，如果一非零向量垂直于一平面，这向量就叫做该平面的法向量。平面上的任一向量均与该平面的法向量垂直。即平面上任一向量与法向量的点乘为0.

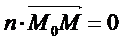
其中n为平面的法向量，M₀M为平面上任两点表示的向量。此式是平面的点法式方程。

由于平面的点法式方程是x,y,z的一次方程，而任一平面都可以用它上面的一点及法向量来确定，所以任一平面都可以用三元一次方程来表示。

Ax+By+Cz+D=0

其中x,y,z的系数就是该平面的一个法向量，即n={A,B,C}。上式就是平面的一般方程。设三个平面的方程分别为：

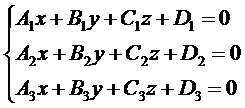
上述三个平面恰交于一点的充分必要条件是方程组有唯一解，即它的系数行列式不等于零：

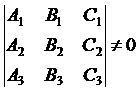
所以求三个平面交点的算法核心是对系数方程组的求解。

2.Algorithm

OpenCASCADE中也有计算三个平面交点的算法，使用类IntAna_Int3Pln。也是使用了直接的算法，即先根据平面的点法式方程计算出平面的一般式，再联立方程组，最后使用高斯Gauss消元法进行求解。其核心代码如下所示：

void IntAna_Int3Pln::Perform (const gp_Pln& P1, const gp_Pln& P2,
const gp_Pln& P3) {
done=Standard_False;
math_Matrix M(1,3,1,3);
math_Vector V(1,3);
P1.Coefficients(M(1,1),M(1,2),M(1,3),V(1));
P2.Coefficients(M(2,1),M(2,2),M(2,3),V(2));
P3.Coefficients(M(3,1),M(3,2),M(3,3),V(3));
math_Gauss Resol(M,gp::Resolution());
if (!Resol.IsDone()) {
empt=Standard_True;
}
else {
empt=Standard_False;
V=-V;
Resol.Solve(V);
pnt.SetCoord(V(1),V(2),V(3));
}
done=Standard_True;
}

算法首先根据平面的点向式数据计算出一般式的参数，使用的类gp_Pln的函数Coefficients()，代码如下所示：

inline void gp_Pln::Coefficients (Standard_Real& A,
Standard_Real& B,
Standard_Real& C,
Standard_Real& D) const
{
const gp_Dir& dir = pos.Direction();
if (pos.Direct()) {
A = dir.X();
B = dir.Y();
C = dir.Z();
}
else {
A = -dir.X();
B = -dir.Y();
C = -dir.Z();
}
const gp_Pnt& P = pos.Location();
D = -(A * P.X() + B * P.Y() + C * P.Z());
}

根据平面的一般方程的定义可知，x,y,z的系数即为平面的法向，所以根据平面的法向量可以确定一般式的系数A、B、C。再代入平面上的任一点计算出D。

最后使用高斯Gauss消元法求解方程组得到三个平面的交点。

3. Conclusion

OpenCASCADE中对三个平面的交点的计算使用了直接的算法，即联立方程组进行求解的方法。从中可以看出这些几何问题在OpenCASCADE中的求解也都是数学的应用题。对方程组的求解，微分、积分等数值方法更是核心中的核心，所以OpenCASCADE将TKMath放在了基础模块。

PDF Version: OpenCASCADE 3 Planes Intersection