图解Leetcode组合总和系列——回溯（剪枝优化）+动态规划

Leetcode组合总和系列——回溯（剪枝优化）+动态规划

组合总和 I

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。

解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,

所求解集为：

[

[7],

[2,2,3]

]

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/combination-sum

此题要求解出所有可能的解，则需要用回溯法去回溯尝试求解，我们可以画一棵解空间树：

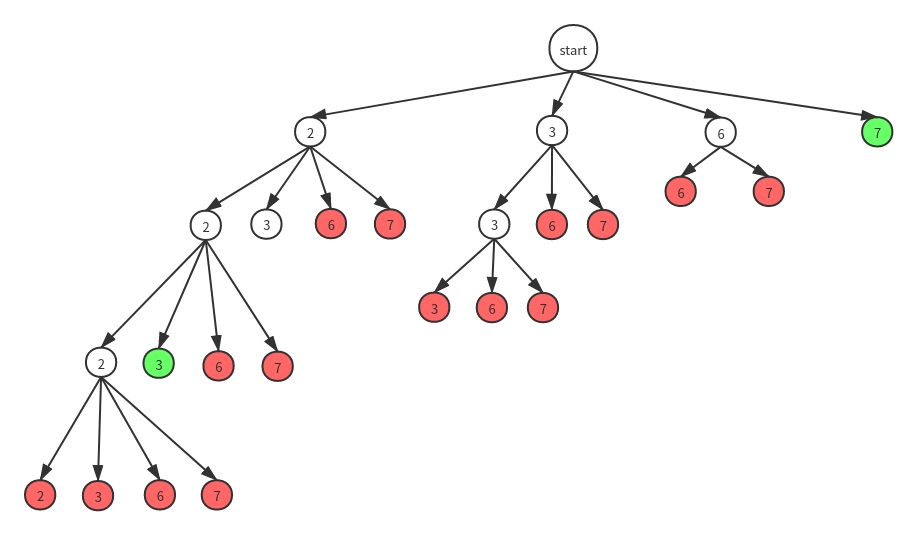
​ 图中绿色节点表示找到了一种可行解，而红色的节点表示到这个节点的时候组合总和的值已经大于target了，无需继续向下尝试，直接返回即可。

​ 因为题目要求解集无重复，即2,2,3和3,2,2应该算作同一种解，所以我们在回溯的时候应该先对candidates数组排序，然后每次只向下回溯大于等于自己的节点。

​ 观察解空间树我们发现：当某一层中第一次出现红色节点或绿色节点后，后面的节点将全变为红色，因为数组是经过排序的，任意节点后面的节点都是大于此节点的（candidates数组无重复元素），所以当出现一个红/绿色节点后，后面的节点不必再继续检查，直接剪枝即可。

剪枝后的解空间树如下：

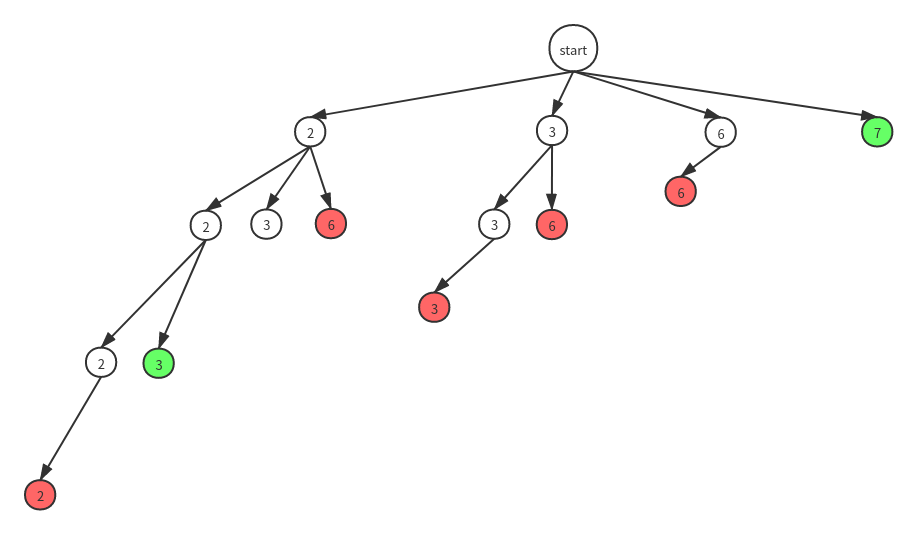
这样看整棵解空间树就小多了，下面直接上代码：

Java版本的回溯解法代码

class Solution {

    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        dfs(candidates,target,0,new ArrayList());
        return result;
    }

    public void dfs (int[] candidates, int target, int currSum, List<Integer> res) {
        if (currSum == target) {
            result.add (new ArrayList(res));
            return;
        }
        for (int i = 0; i < candidates.length; i++) {
            if (currSum + candidates[i] > target) {
                return;
            }
            int size = res.size();
            if (size==0 || candidates[i] >= res.get(size-1)) {
                res.add(candidates[i]);
                dfs(candidates, target, currSum+candidates[i],res);
                res.remove(size);
            }
        }
    }
}

Go版本的回溯解法代码

func combinationSum(candidates []int, target int) (result [][]int) {
    sort.Ints(candidates)
	var dfs func(res []int, currSum int)
	dfs = func(res []int, currSum int) {
		if currSum == target {
			result = append(result, append([]int(nil), res...))
			return
		}
		for i := 0; i < len(candidates); i++ {
			if currSum + candidates[i] > target {
				return
			}
			if len(res) == 0 || candidates[i] >= res[len(res)-1] {
				length := len(res)
				res = append(res, candidates[i])
				dfs(res, currSum+candidates[i])
				res = res[:length]
			}
		}
	}
	var res []int
	dfs(res, 0)
	return
}

组合总和 II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。

解集不能包含重复的组合。

示例 1:

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/combination-sum-ii

和组合总和I不同的是这个题目中的candidates数组中出现了重复数字，而且每个数字只能使用一次，我们对这个数组进行排序，每次回溯进下一层的时候都从上一层访问的节点的下一个开始访问。画出的解空间树如下：

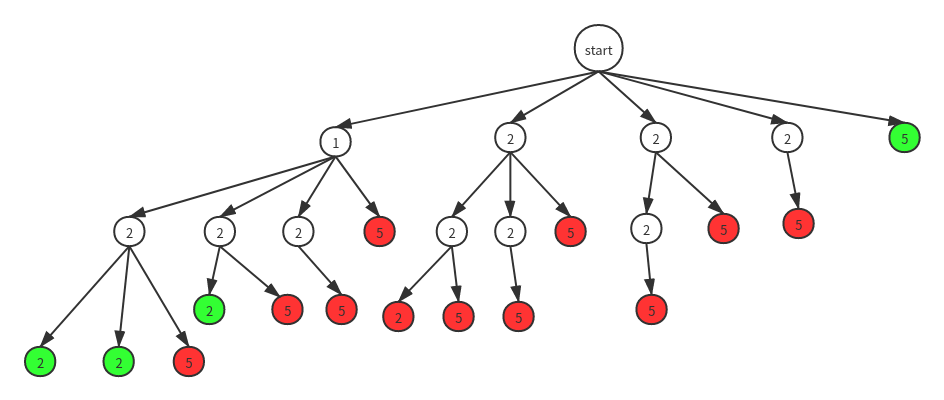
观察解空间树发现还是有重复的解出现，比如1,2,2出现了两次，这种问题我们可以通过两种方法来解决

1. 每次当找到一个可行解后，判断看是否此解已经存在于之前发现的解中了，如果存在就丢弃

2. 剪枝，同一层中同样的节点只能出现一次，这样不但整个解空间树会小很多，而且避免了判断时候的开销，下面是剪枝后的解空间树

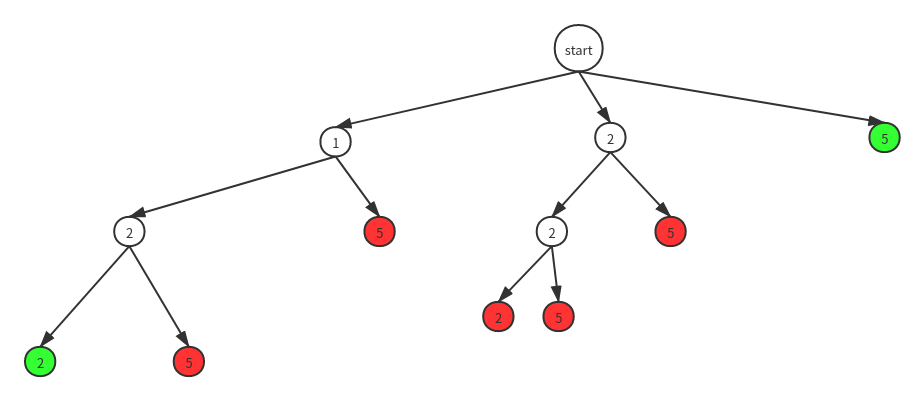
具体剪枝的方法我们可以通过增加一个visit集合，记录同一层是否出现过相同节点，如果出现过就不再次访问此节点。

我对两种解法做了对比，执行的时间效率对比如下：第一种对应上面的结果，第二种解法对应下面的结果

下面贴出第二种解法的代码：

Java版本的回溯解法代码

class Solution {

    public static void trace(List<List<Integer>> result, List<Integer> res, int[] candidates, int target, int curr, int index) {
        if (curr == target) {
            //得到预期目标
            result.add(new ArrayList<>(res));
        }
        Set<Integer> visit = new HashSet<>();
        for (int j = index+1; j < candidates.length; j++) {
            if (visit.contains(candidates[j])) {
                continue;
            } else {
                visit.add(candidates[j]);
            }
            if (curr + candidates[j] > target){
                //此路不通，后路肯定也不通
                break;
            } else {
                //继续试
                res.add(candidates[j]);
                int len = res.size();
                trace(result, res,candidates,target,curr+candidates[j],j);
                res.remove(len-1);
            }
        }
    }

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        List<Integer> res = new ArrayList<>();
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        int curr = 0;
        Arrays.sort(candidates);
        trace(result, res,candidates,target,curr,-1);
        return result;
    }
}

Go版本的回溯解法代码

func combinationSum2(candidates []int, target int) (result [][]int) {
	sort.Ints(candidates)
	var dfs func(res []int, currSum, index int)
	dfs = func(res []int, currSum, index int) {
		if currSum == target {
			result = append(result, append([]int(nil), res...))
			return
		}
		var set []int
		for i := index+1; i < len(candidates); i++ {
			if isExist(set, candidates[i]) {
				continue
			} else {
				set = append(set, candidates[i])
			}

			if currSum + candidates[i] > target {	//遇到红色节点，直接跳出循环，后面也无需尝试
				break
			} else {
				res = append(res, candidates[i])
				dfs(res, currSum+candidates[i], i)
				res = res[:len(res)-1]
			}
		}
	}
    var res []int
    dfs(res, 0, -1)
	return
}

func isExist(set []int, x int) bool {
	for _, v := range set {
		if v == x {
			return true
		}
	}
	return false
}

组合总和 III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。

解集不能包含重复的组合。

示例 1:

输入: k = 3, n = 7

输出: [[1,2,4]]

示例 2:

输入: k = 3, n = 9

输出: [[1,2,6], [1,3,5], [2,3,4]]

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/combination-sum-iii

此题的candidates数组不再由题目给出，而是由[1,9]区间里的数组成，且每种组合不存在重复的数，则每种数字只能用一次，我们还是继续采用回溯法，不同的是限制了解集中数字的个数。而且每层的回溯都从上一层访问的节点的下一个节点开始。

如果使用暴力法去回溯，将得到下面这样的一棵解空间树（由于树过大，所以右边被省略）

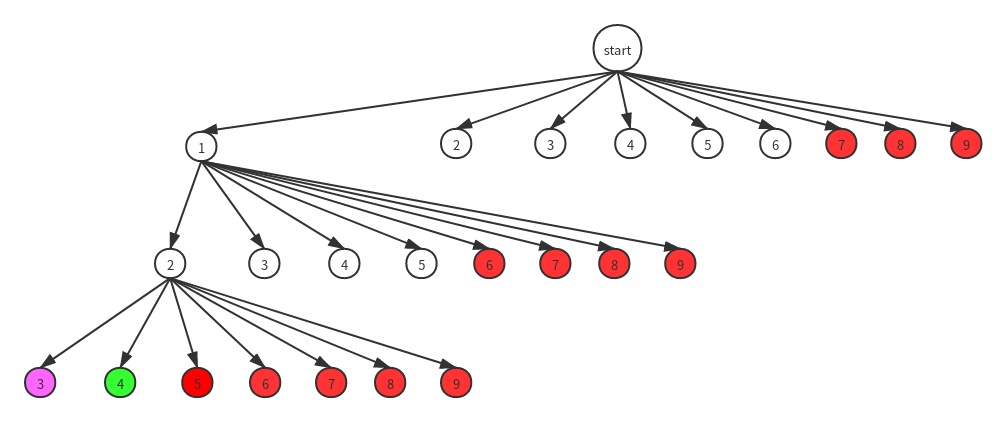
因为题目中规定了树的深度必须是k，红色表示不可能的解，绿色表示可行解，紫色表示到了规定的层数k，但总和小于n的情况。

观察上述的解空间树我们发现了剪枝的方法：

1. 对于红色节点之后的节点直接裁剪掉
2. 但需要注意紫色的虽然不符合题意，但由于后面可能出现正确解，所以不能剪掉
3. 根据树的深度来剪，上面两个题中都没有规定深度，此题还可以根据深度来剪，如果超过规定深度就不继续向下探索

画出剪枝后的解空间树（同样省略了右边的树结构）：

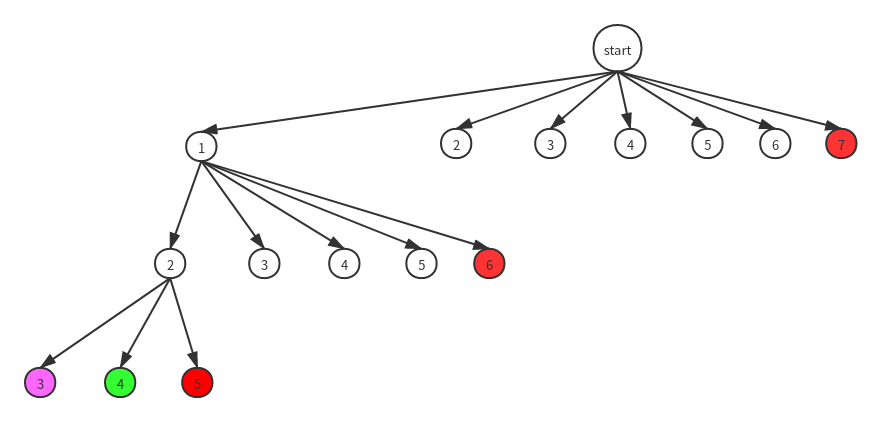
Java版本的回溯解法代码

class Solution {
    public List<List<Integer>> combinationSum3(int k, int n) {
        List<Integer> res = new ArrayList<>();
        List<List<Integer>> result = new ArrayList<List<Integer>>();
        trace(result,res,0,k,n);
        return result;
    }

    public void trace (List<List<Integer>> result, List<Integer> res, int curr, int k, int n) {
        if (res.size() == k && curr == n) {
            result.add(new ArrayList<>(res));
            return;
        } else if (res.size() < k && curr < n) {
            for (int i = 1; i < 10; i++) {
                int len = res.size();
                if (len == 0 || i > res.get(len - 1)) {
                    res.add(i);
                    trace(result,res,curr+i,k,n);
                    res.remove(len);
                }
            }
        } else {        //树的深度已经大于规定的k
            return;
        }
    }
}

Go版本的回溯解法代码

func combinationSum3(k int, n int) (result [][]int) {
	var dfs func(res []int, currSum int)
	dfs = func(res []int, currSum int) {
		if len(res) == k && currSum == n {
			result = append(result, append([]int(nil), res...))
			return
		} else if len(res) < k && currSum < n {
			i := 1
			if len(res) > 0 {
				i = res[len(res)-1]+1
			}
			for ; i < 10; i++ {
				res = append(res, i)
				dfs(res, currSum+i)
				res = res[:len(res)-1]
			}
		} else {		//搜索的深度已经超过了k
			return
		}
	}
	var res []int
	dfs(res, 0)
	return
}

组合总和 IV

给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

示例 1：

输入：nums = [1,2,3], target = 4

输出：7

解释：

所有可能的组合为：

(1, 1, 1, 1)

(1, 1, 2)

(1, 2, 1)

(1, 3)

(2, 1, 1)

(2, 2)

(3, 1)

请注意，顺序不同的序列被视作不同的组合。

示例 2：

输入：nums = [9], target = 3

输出：0

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/combination-sum-iv

这个道题目并没有像上面一样要求我们找出所有的解集，而是只要求解解的个数，这时如果我们再采用回溯法去求解无疑是造成了很大的浪费，所以考虑使用动态规划，只求解个数而不关注所有解的具体内容。

题目允许数字的重复，且对顺序敏感（即不同顺序视做不同解），这样我们可以通过让每一个nums数组中数num做解集的最后一个数，这样当x作为解集的最后一个数，解集就为num1,num2,num3......x

如果dp数组的dp[x]表示target为x时候的解集个数，那么我们只需要最后求解dp[target]即可。

那么当最后一个数为x时对应的解集个数就为dp[target-x]个，让nums中的每一个数做一次最后一个数，将结果相加就是dp[target]的值，不过需要注意的是dp[0] = 1表示target为0时只有一种解法（即一个数都不要），dp的下标必须为非负数。

下面是状态转移方程（n为nums最后一个元素的下标）：

\[dp[i]=
\begin{cases}
1& \text{i=0}\\
\sum_{j=0}^n\ dp[target-nums[j]& \text{i!=0 && target-nums[j] > 0}
\end{cases}
\]

Java版本的动态规划解法代码

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0] = 1;
        for (int i = 1; i <= target; i++) {
            for (int num:nums) {
                int tmp = i - num;
                if (tmp >= 0) {
                    dp[i] += dp[tmp];
                }
            }
        }
        return dp[target];
    }
}

Go版本的动态规划解法代码

func combinationSum4(nums []int, target int) int {
	dp := make([]int, target+1)
	dp[0] = 1
	for i := 1; i <= target; i++ {
		for _, v := range nums {
			tmp := i - v
			if tmp >= 0 {
				dp[i] += dp[tmp]
			}
		}
	}
	return dp[target]
}