Paper | Adaptive Computation Time for Recurrent Neural Networks

目录

• 1. 网络资源
• 2. 简介
• 3. 自适应运算时间
  • 3.1 有限运算时间
  • 3.2 误差梯度

1. 网络资源

这篇文章的写作太随意了，读起来不是很好懂（掺杂了过多的技术细节）。因此有作者介绍会更好。

B站有视频：https://www.bilibili.com/video/av66005226/

动机：RNN（LSTM，GRU等）在处理一句话时，对每一个token的计算量是相同的。然而事实上每一个token的重要性不一。

因此，本文考虑在另一个维度：在每个cell的内部，进行差异化改造。

2. 简介

本文提出了一个自适应运算时间（adaptive computation time, ACT）的概念，即让RNN学习应该要用多少时间进行某个任务的运算。ACT可差分、鉴别式，很容易嵌入网络。

所谓计算量，对于前向网络而言，可以用网络深度来控制；对于循环网络，可以用输入序列的长度来控制。深度的增加可以让前向网络性能更好，这一点已经毋容置疑[5,4,19,9]；输入循环网络的序列长度的提升 也能带来类似的收益[31,33,25]。但至今仍然没有试验可以告诉我们：多少运算量是合适的。并且，很多人在尝试缓解梯度消失问题。实际上，合理地减小运算量也是一种缓解办法。

具体而言，本文在网络输出端和隐含状态端增加了一个归一化的（sigmoidal）停止单元（halting unit）。[7]采取了一种采样的方法来实现停止决策，称为mean-field approach。但作者认为其平滑函数不参与随机梯度预测，性能上可能不够好。【具体没看懂】

A stochastic alternative would be to halt or continue according to binary samples drawn from the halting distribution—a technique that has recently been applied to scene understanding with recurrent networks [7]. However the mean-field approach has the advantage of using a smooth function of the outputs and states, with no need for stochastic gradient estimates. We expect this to be particularly beneficial when long sequences of halting decisions must be made, since each decision is likely to affect all subsequent ones, and sampling noise will rapidly accumulate (as observed for policy gradient methods [36]).

此外还有一个相关的工作，自限制神经网络[26,30]。其在一个大型的、部分激活的网络中采用了一个停止神经元来结束更新。在该网络中，停止仅仅取决于一个激活值阈值，而没有相关的梯度传递。

广义地说，学会停止是一种有条件计算（conditional computation），即网络的一部分选择性地开启或关闭[3,6]。这种对最小运算量的搜寻，本质上是一个科氏复杂度[21]计算工作。而本文采取的是一种实用的做法：将时间成本作为损失的一部分，来鼓励高效学习。缺点是，关于时间成本的权重需要人为设定。

3. 自适应运算时间

设\(\mathcal{R}\)是循环神经网络；\(\mathcal{S}\)是状态转换模型，状态序列是\(\mathbf{s}=\left(s_{1}, \dots, s_{T}\right)\)；输出是\(\mathbf{y}=\left(y_{1}, \dots, y_{T}\right)\)，输出权值和偏置分别是\(W_{y}\)和\(b_y\)；输入序列是\(\mathbf{x}=\left(x_{1}, \dots, x_{T}\right)\)，输入权值是\(W_{x}\)，则有：
\[
\begin{array}{l}{s_{t}=\mathcal{S}\left(s_{t-1}, W_{x} x_{t}\right)} \\
{y_{t}=W_{y} s_{t}+b_{y}}\end{array}
\]

其中的状态序列是固定长度的。对于LSTM而言，状态还包括记忆细胞【控制门】的状态。在NTM中也有类似的结构。这些与中间记忆有关的状态不会直接联系到最终输出。

RNN如图，其中的\(W\)和\(\mathcal{S}\)是共享的。

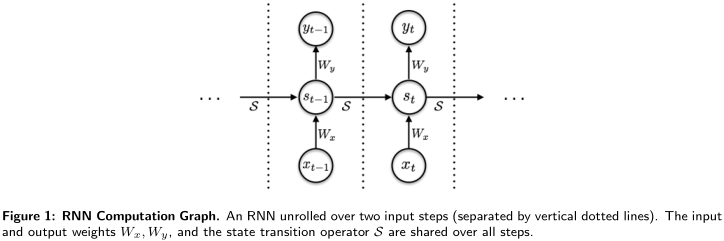
本文提出的ACT的做法如图。图中指向box的箭头说明该操作引用于box中所有元素；离开box的箭头说明box中元素先求和。

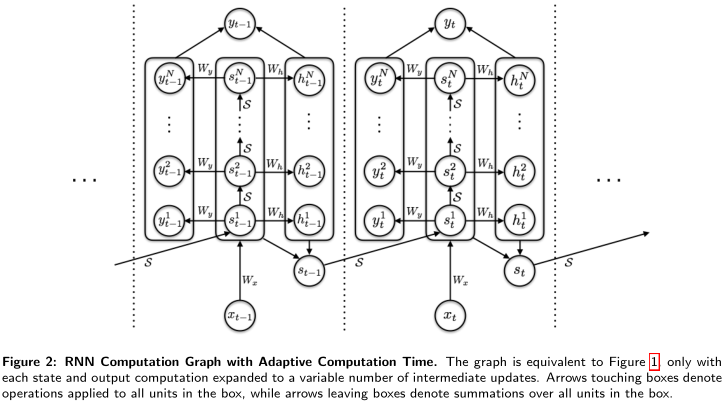
如图，在任意\(t\)时刻，状态都要转换\(N(t)\)次，即有中间状态序列\(\left(s_{t}^{1}, \ldots, s_{t}^{N(t)}\right)\)。对应地，输出也要转换\(N(t)\)次，即有中间输出序列\(\left(y_{t}^{1}, \ldots, y_{t}^{N(t)}\right)\)。此时整体RNN表达式变成：
\[
s_{t}^{n}=\left\{\begin{array}{l}{\mathcal{S}\left(s_{t-1}, x_{t}^{1}\right) \text { if } n=1} \\ {\mathcal{S}\left(s_{t}^{n-1}, x_{t}^{n}\right) \text { otherwise }}\end{array}\right.
\\ y_{t}^{n}=W_{y} s_{t}^{n}+b_{y}
\]

【公式里的\(x_t^n\)实际上都是\(x_t\)？因为箭头指向box】

此时，我们再引入停止单元\(h\)。其推理过程很简单：
\[
h_{t}^{n}=\sigma\left(W_{h} s_{t}^{n}+b_{h}\right)
\]

那么如何决策停止呢？也很简单，输出\(h\)累积达到\(1 - \epsilon\)即可。\(\epsilon\)在本文中取0.01。因此，最早达到\(1 - \epsilon\)的\(n = N(t)\)。为什么要设置\(\epsilon\)呢？如果强制要求达到1，那么至少需要两步才能停止。我们希望最少一步就能停止。

注意，图中的矩阵和转移模型仍然是广泛共享的。

根据这种停止机制，我们就能定义停止概率分布：
\[
p_{t}^{n}=\left\{\begin{array}{l}{1-\sum_{n=1}^{N(t)-1} h_{t}^{n} \text { if } n=N(t)} \\ {h_{t}^{n} \text { otherwise }}\end{array}\right.
\]

最终的状态和输出采用加权求和的方式得到：
\[
s_{t}=\sum_{n=1}^{N(t)} p_{t}^{n} s_{t}^{n}\\
y_{t}=\sum_{n=1}^{N(t)} p_{t}^{n} y_{t}^{n}
\]

其实还有一种方案：采样，即选取一种合理的采样方法，从\(s_t^n\)和\(y_t^n\)中抽样即可。但这样有两个问题：（1）采样方法要足够合理；（2）采样容易受到噪声干扰。

作者还蛮严谨，给出了这种线性假设的理由。在论文第四页。

3.1 有限运算时间

很简单，作者单独设置了一个“思考”损失：
\[
\mathcal{P}(\mathrm{x}) = \sum_{t=1}^{T} \rho_{t} = \sum_{t=1}^{T} (N(t) + R(t))
\]
其中\(R(t)=1-\sum_{n=1}^{N(t)-1} h_{t}^{n}\)。

解释：惩罚转移步数和最后一步的概率。我们希望最后一步的概率不那么大。并且所有时间步的惩罚求和。

最后的损失函数是二者之和，并且由参数\(\tau\)调控：
\[
\hat{\mathcal{L}}(\mathbf{x}, \mathbf{y})=\mathcal{L}(\mathbf{x}, \mathbf{y})+\tau \mathcal{P}(\mathbf{x})
\]

实验发现，网络性能对于该参数极其敏感。作者也没有很好的选择方法。

3.2 误差梯度

要注意，\(\rho_{t}\)是关于停止输出\(h\)不连续的。主要是因为关于\(N(t)\)不连续。但除了最后\(n = N(t)\)的瞬间，其他时刻是连续的。我们直接让该点梯度为0。其余点梯度正常为-1：
\[
\frac{\partial \mathcal{P}(\mathbf{x})}{\partial h_{t}^{n}}=\left\{\begin{array}{l}{0 \text { if } n=N(t)} \\ {-1 \text { otherwise }}\end{array}\right.
\]

最终能推导出：
\[
\frac{\partial \hat{\mathcal{L}}(\mathbf{x}, \mathbf{y})}{\partial h_{t}^{n}}=\left\{ \begin{array}{l}{
\frac{\partial \mathcal{L}(\mathbf{x}, \mathbf{y})}{\partial y_{t}}\left(y_{t}^{n}-y_{t}^{N(t)}\right)+\frac{\partial \mathcal{L}(\mathbf{x}, \mathbf{y})}{\partial s_{t}}\left(s_{t}^{n}-s_{t}^{N(t)}\right)-\tau \text { if } n < N(t)} \\ {0 \text { if } n = N(t)}\end{array}\right.
\]

实验略。