Bezier曲线的实现——de Casteljau算法
这学期同时上了计算机图形学和计算方法两门课,学到这部分的时候突然觉得de Casteljau递推算法特别像牛顿插值,尤其递推计算步骤很像牛顿差商表。
一开始用伯恩斯坦多项式计算Bezier曲线的时候,由于其多项式的计算十分不利于计算机实现,还会出现数值不稳定的情况
所以后来出现了de Casteljau算法,以下PPT截图来自北京化工大学李辉老师
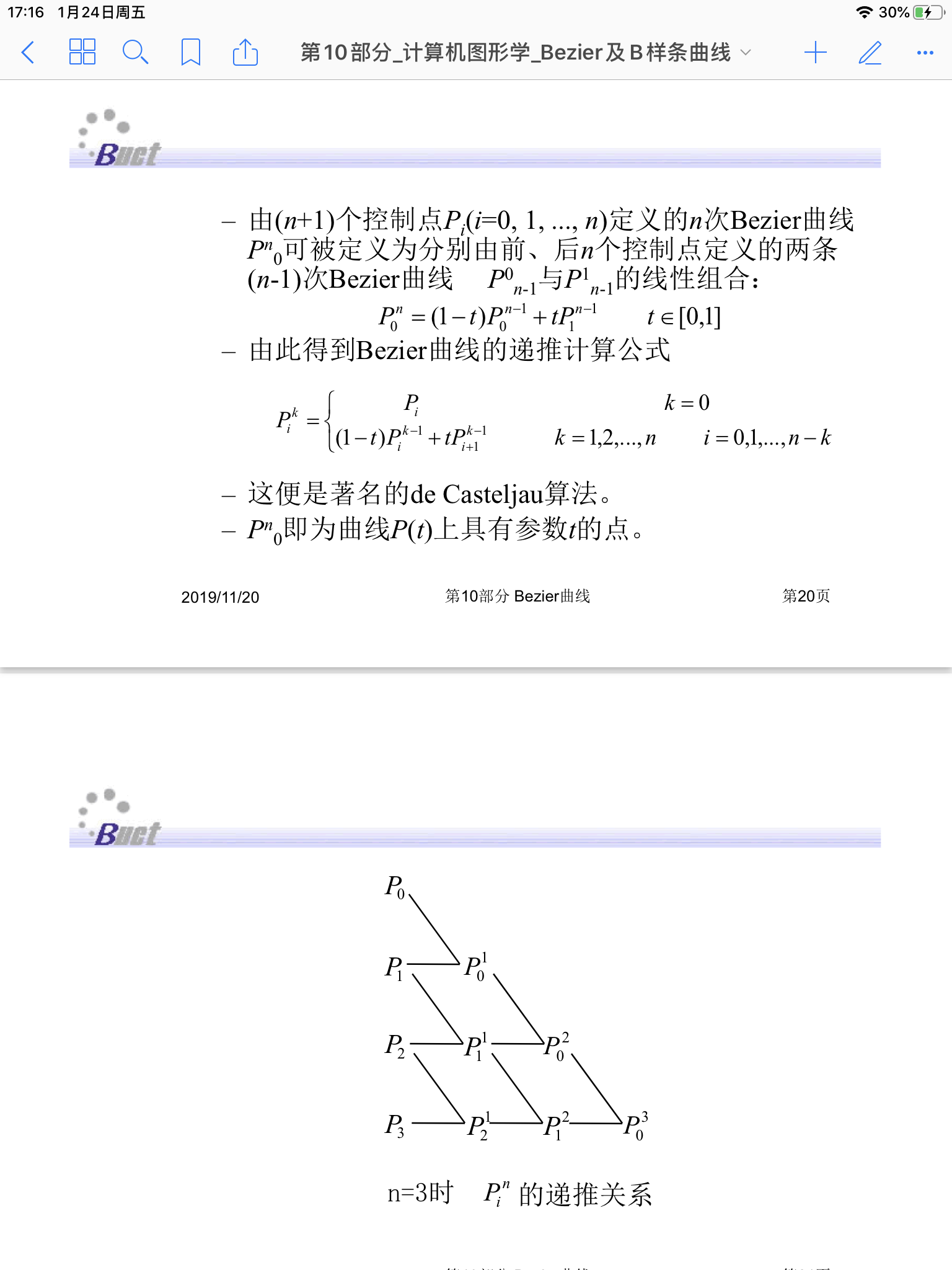
实现代码(六个顶点):
import numpy as np
import matplotlib.pyplot as plt #B = (1-t)*P0+t*P1
def one_bezier_curve(a, b, t):
return (1-t)*a + t*b #使用de Casteljau算法求解曲线
def n_bezier_curve(x, n, k, t):
#当且仅当为一阶时,递归结束
if n == 1:
return one_bezier_curve(x[k], x[k+1], t)
else:
return (1-t)*n_bezier_curve(x, n-1, k, t) + t*n_bezier_curve(x, n-1, k+1, t) def bezier_curve(x, y, num, b_x, b_y):
#n表示阶数
n = len(x) - 1
t_step = 1.0 / (num - 1)
t = np.arange(0.0, 1+t_step, t_step)
for each in t:
b_x.append(n_bezier_curve(x, n, 0, each))
b_y.append(n_bezier_curve(y, n, 0, each)) if __name__ == "__main__":
x = [int(n) for n in input('x:').split()]
y = [int(n) for n in input('y:').split()]
plt.plot(x, y)
# x = [0, 2, 5, 10, 15, 20]
# y = [0, 6, 10, 0, 5, 5]
num = 100
b_x = []
b_y = []
bezier_curve(x, y, num, b_x, b_y)
plt.plot(b_x, b_y) plt.show()
运行截图:
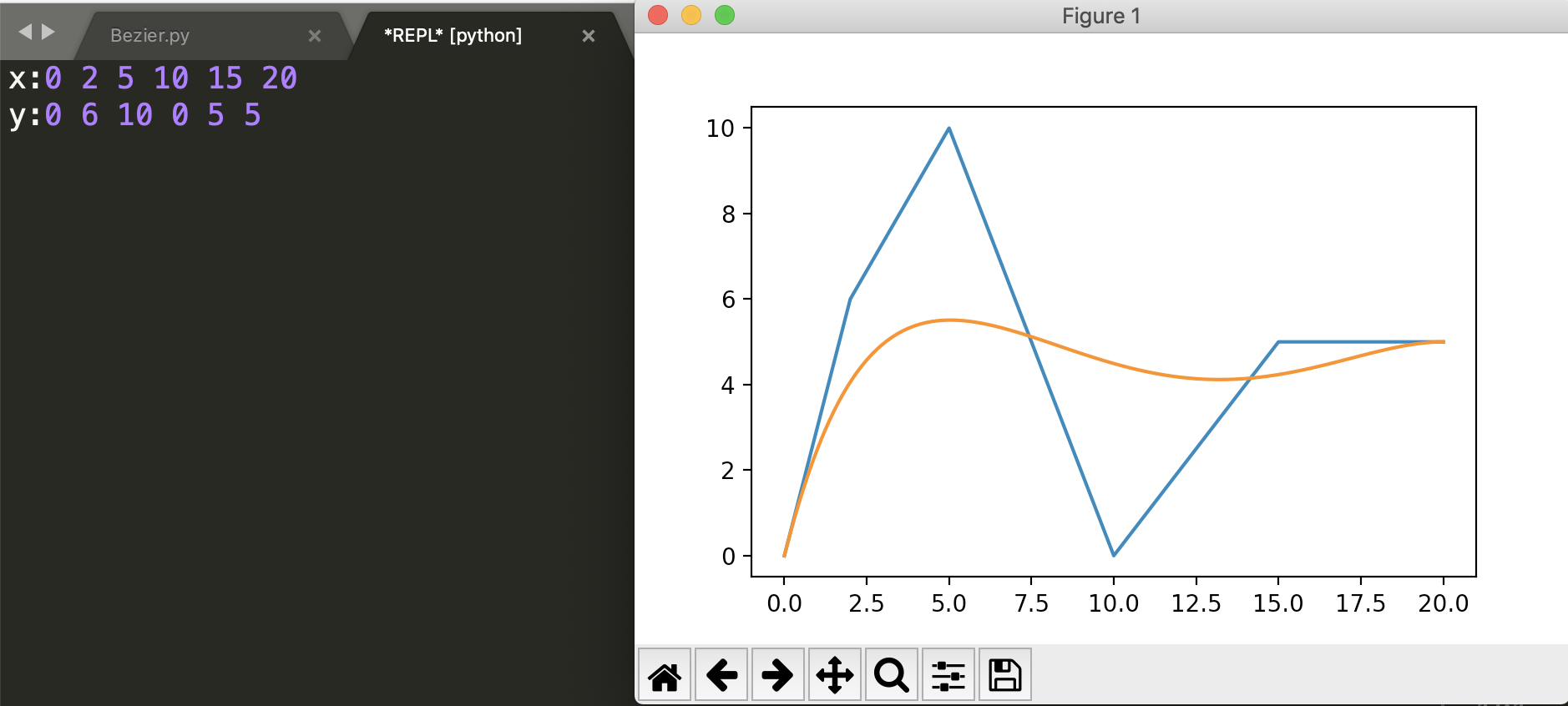
Bezier曲线的实现——de Casteljau算法的更多相关文章
- C# 实现Bezier曲线(vs2008)
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...
- 曲线生成与求交—Bezier曲线
Bezier曲线生成 法国工程师Pierre Bezier在雷诺公司使用该方法来设计汽车.一条Bezier曲线可以拟合任何数目的控制点. 公式 设\(n+1\)个控制点\(P_0,P_1--P_n\) ...
- Bezier曲线的原理 及 二次Bezier曲线的实现
原文地址:http://blog.csdn.net/jimi36/article/details/7792103 Bezier曲线的原理 Bezier曲线是应用于二维图形的曲线.曲线由顶点和控制点组成 ...
- 连续bezier曲线的实现
需求场景 一系列的坐标点,划出一条平滑的曲线 3次Bezier曲线 基本上大部分绘图工具都实现了3次Bezier曲线,4个点确定一条3次Bezier曲线.以html5中的canvas为例 let ct ...
- 实验6 Bezier曲线生成
1.实验目的: 了解曲线的生成原理,掌握几种常见的曲线生成算法,利用VC+OpenGL实现Bezier曲线生成算法. 2.实验内容: (1) 结合示范代码了解曲线生成原理与算法实现,尤其是Bezier ...
- 插入2D点,在WPF中使用Bezier曲线
原文Interpolate 2D points, usign Bezier curves in WPF Interpolate 2D points, usign Bezier curves in WP ...
- 简单而粗暴的方法画任意阶数Bezier曲线
简单而粗暴的方法画任意阶数Bezier曲线 虽然说是任意阶数,但是嘞,算法原理是可以到任意阶数,计算机大概到100多阶就会溢出了 Bezier曲线介绍] [本文代码] 背景 在windows的Open ...
- [摘抄] Bezier曲线、B样条和NURBS
Bezier曲线.B样条和NURBS,NURBS是Non-Uniform Rational B-Splines的缩写,都是根据控制点来生成曲线的,那么他们有什么区别了?简单来说,就是: Bezier曲 ...
- 7.5.5编程实例-Bezier曲线曲面绘制
(a)Bezier曲线 (b) Bezier曲面 1. 绘制Bezier曲线 #include <GL/glut.h> GLfloat ct ...
随机推荐
- netty权威指南学习笔记一——NIO入门(3)NIO
经过前面的铺垫,在这一节我们进入NIO编程,NIO弥补了原来同步阻塞IO的不足,他提供了高速的.面向块的I/O,NIO中加入的Buffer缓冲区,体现了与原I/O的一个重要区别.在面向流的I/O中,可 ...
- [JZOJ]3413.KC的瓷器
Description KC来到了一个盛产瓷器的国度.他来到了一位商人的店铺.在这个店铺中,KC看到了一个有n(1<=n<=100)排的柜子,每排都有一些瓷器,每排不超过100个.那些精美 ...
- 十一、JavaScript之两种注释方法
一.代码如下 二.运行效果如下
- 七十二、SAP中内表的修改,添加条件语句,多条目修改
一.代码如下 二.MODIFY执行前断点数据 三.查看到数据如下 四.往下单步走一步,发现有3条数据被修改 五.执行后修改如下
- Spark 资源调度包 stage 类解析
spark 资源调度包 Stage(阶段) 类解析 Stage 概念 Spark 任务会根据 RDD 之间的依赖关系, 形成一个DAG有向无环图, DAG会被提交给DAGScheduler, DAGS ...
- vue学习(三)组件传值
组件 官网(https://cn.vuejs.org/v2/guide/components.html) 组件分为局部组件和全局组件 局部组件:是内容中国的一部分 只是在当前组件加载的时候 全部组件: ...
- css 径向渐变
.example { width: 150px; height: 80px; background: -webkit-radial-gradient(red, green, blue); /* Saf ...
- Jetson TX2 安装JetPack3.3教程
Jetson TX2 刷机教程(JetPack3.3版本) 参考网站:https://blog.csdn.net/long19960208/article/details/81538997 版权声明: ...
- jvm 优化
1.jvm 运行参数 1.1 jvm 参数类型 1.1.1 标准参数 -help -version 1.1.2 -X参数(非标准参数) -Xint -Xcomp 1.1.3-XX参数(使用率高) -X ...
- 调用servlet报The requested resource is not available.
调用servlet的时候经常有这种报错,一般来说我直到现在遇到的情况大致有以下几类: 1.参数写错了 在新创建的servlet文件中有这么一行代码,“/LoginCheck”这个一定要和form表单中 ...
