杭州集训Day5

下面是Day5的题目！（其实都咕了好几天了

100+70+40=210.

T1 皇后 XY 的疑难 _{(1s 512MB)}

1.1 题目描述

有一个n*n的王国城堡地图上，皇后XY喜欢看骑士之间的战斗，于是他准备布置m个骑士，其中

每一个骑士都可以向8个方向，上、下、左、右、左上、左下、右上、右下移动若干距离。且每一个骑士都可以攻击他八个方向上离它最近的骑士。

皇后XY等不及看骑士之间的对决，但他又担心骑士的安危，她想提前知道每一个骑士会被从几个方向攻击到，设为 s。很显然 s 属于[0,8] 。最后要求出来 num[0]，num[1] ……num[8] 九个数，表示有多少骑士被攻击到0次，1次……8次。数据保证m个骑士中任意两个不在同一个位置。

1.2 输入格式

第一行两个正整数 n,m（n,m≤10⁵），然后接下来m行，每一行x[i]，y[i] 分别表示第i个骑士的

横坐标和纵坐标。1≤x[i],y[i]≤n。

1.3 输出格式

一行9个整数，分别为 num[0]，num[1]……num[8] ，两个数中间用空格隔开。

1.4 样例输入

8 4
4 3
4 8
6 5
1 6

1.5 样例输出

0 3 0 1 0 0 0 0 0

1.6 数据约定

对于 30%的数据，n,m≤1000。

对于 60%的数据， n≤100000，m≤1000。

对于 100%的数据， n,m<=100000，1≤x[i],y[i]≤n 。

这不就是皇后的攻击方式吗

所以我们很容易想到“八皇后”那题的写法

就是用四个数组分别存每行，每列，每个左斜线(x-y)，每个右斜线(x+y)的骑士个数

但是这题要求每个骑士八个方向上有没有别的骑士

就不能只用四个数组了

要用八个数组存八个方向的最大值

比如说第i列的最上面的骑士和最下面的骑士的纵坐标

这样的话在这一列的骑士的纵坐标如果大于最下面的就说明他不是最下面的

说明他下面还有人

如果其纵坐标小于最上面的就说明他不是最上面的

也就说明他上面还有人

然后注意下左斜线的x-y不能为负数，所以统一加个N即可（还要注意下数组大小

很简单的一题，时间复杂度为O(n)

T2 快来 pick sxk_{(1s 512MB)}

2.1 题目描述
千古神犇邵徐坤 sxk，他现在利用自己猴子的属相变成了n个会打篮球的分身，每个会打篮球的分身都
有一个鸡儿你真美值，这些分身是乱序的。
你需要将其按鸡儿你真美值从小到大排序，每次你可以将一个分身揪到任意一个位置（某两个分身中
间），代价是你要掉该分身的鸡儿你真美值的毛。
为了不变成sxk这样的聪明"绝顶"的大猴子，你要以尽量少的代价完成这个任务，你需要回答每一次
分身后你会掉的最少毛数。
2.2 输入格式
从文件pick.in中读入数据。
数据的第1行包含一个非负整数t表示sxk分身的次数。
对于每一组数据
第1行包含一个非负整数n表示分身的个数
第2行包含n个数，a_i表示第i个分身的鸡儿你真美值
2.3 输出格式
输出到文件pick.out中。
对于每一个询问输出一个整数，表示你最少会掉的毛数
2.4 样例输入

9 5 7 2 8

7 6 5 4 3

2.5 样例输出

18
2.6 数据约定
对于30%的数据满足 Σn≤1000.
对于另外30%的数据满足 a_i>a_i+1.
对于100%的数据满足 Σn≤200000，a_i≤10⁷.

很显然每个数要移的话一次就够了

这样的话问题就被转化成了

“删除一些数，使得剩下的数刚好成不下降序列，要删除的数总和尽量小”

即“求最大权值不下降子序列”

前30%的数据O(n²)dp就可以了（f[i]=max{f[j]}+a[i],j<i,a[j]<=a[i]）

a_i>a_i+1的30%数据很显然答案就是a₂+a₃+...+a_n

接下来考虑100分做法

其实也不难，就是把dp优化成O(nlog n)的就行了，

把f[i]用权值线段树维护一下，

查a[j]<=a[i]中f[j]的最大值还是很好求的

下面是代码：

#include<bits/stdc++.h>

#define Lowbit(i) (i&(-i))

#define ll long long

using namespace std;

const int N=2e5+1e4;

int n,a[N],b[N],p[N*]; ll w[N];

ll Max(ll x,ll y){

    return x>y?x:y;

}

int rd(){

    int s=,ff=;

    char w=getchar();

    while(w<''||w>''){

        if(w=='-') ff=-;

        w=getchar();

    }

    while(w>=''&&w<=''){

        s=s*+(w-'');

        w=getchar();

    }

    return s*ff;

}

ll Query(int x){ ll maxn=;

    for(int i=x;i;i-=Lowbit(i))

        maxn=Max(maxn,w[i]);

    return maxn;

}

void Add(int x,ll y){

    for(int i=x;i<=n;i+=Lowbit(i))

        w[i]=Max(w[i],y);

}

int main(){

//    freopen("pick.in","r",stdin);

//    freopen("pick.out","w",stdout);

    int t=rd();

    while(t--){ n=rd(); int fla=; ll tot=;

        for(int i=;i<=n;i++)

            a[i]=rd(),b[i]=a[i],tot+=a[i];

        sort(b+,b++n); int ct=;

        for(int i=;i<=n;i++){

            if(i==||b[i]!=b[i-]) ct++;

            p[b[i]]=ct;

        }

        ll maxn=-1e17;

        for(int i=;i<=n;i++){

            ll f=Query(p[a[i]]); Add(p[a[i]],f+a[i]);

//            for(int j=1;j<i;j++)

//                if(a[j]<=a[i])

//                    f[i]=Max(f[i],f[j]+a[i]);

            maxn=Max(maxn,f+a[i]);

        }

        for(int i=;i<=n;i++) p[a[i]]=,w[i]=;

        printf("%lld\n",tot-maxn); continue;

    }

    return ;

}

对了，我订正的时候用的是树状数组，

因为是求前缀的最大值，所以树状数组是可以的，

记住区间求最大值千万不能用树状数组。

T3 一道另类的前缀和_{(1s 512MB)}

3.1 题目描述

已知常数 n，k ，p 和函数

你需要计算该函数的前缀和S(n)对p取模的结果

3.2 输入格式

从文件prefix.in中读入数据。

数据的第1行包含三个非负整数 n，k ，意义如题目描述。

3.3 输出格式

输出到文件prefix.out中。输出一行一个正整数，S(n)可能为分数，所以输出S(n)对p取模的结

果。

即S(n)=a/b输出a*b^-1.

3.4 样例输入

5 2 998244353

3.5 样例输出

465847367

3.6 数据约定

对于100%的数据n≤10⁷，k≤10⁷，k≤n.

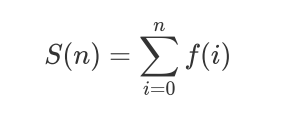
一道数论题，先推式子：

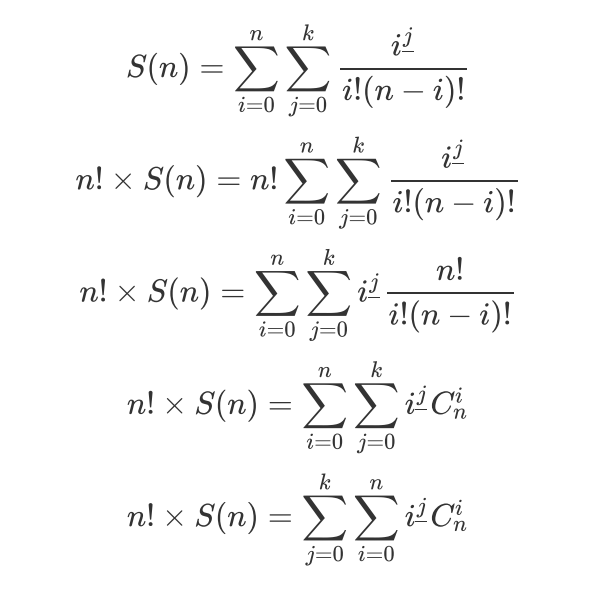
现在求出即可

前20%的n≤2000，预处理下，直接这样模拟就行了

再来看k=0，由二项式定理得：

S(n)就可以算出来了

到这里你就可以获得40分的好成绩，当然还不够，

要继续的话，我得先引出一个推论：

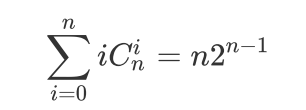
证明如下：

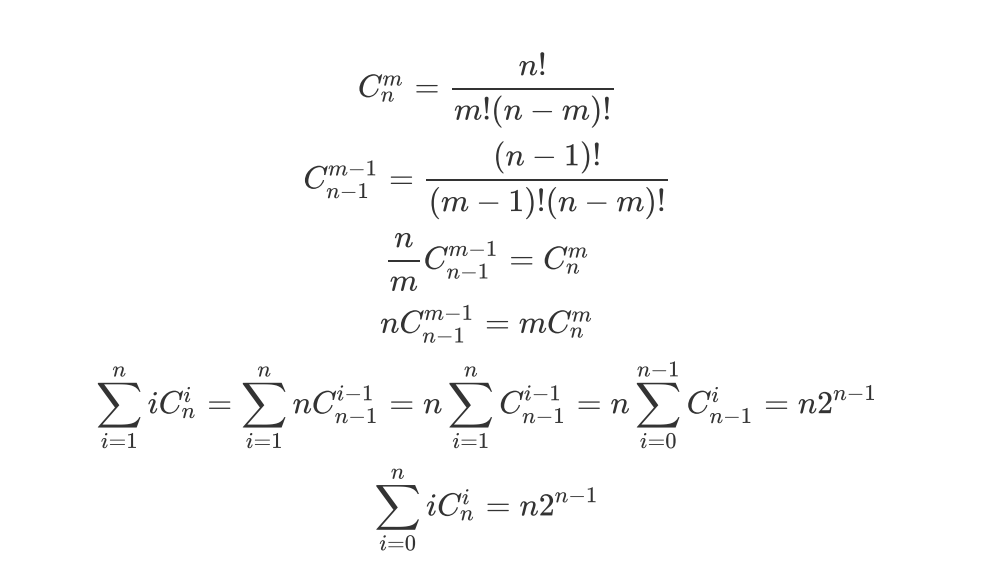
k=1就可以了

很简单对吧，我们继续

先模拟下k=2的情况

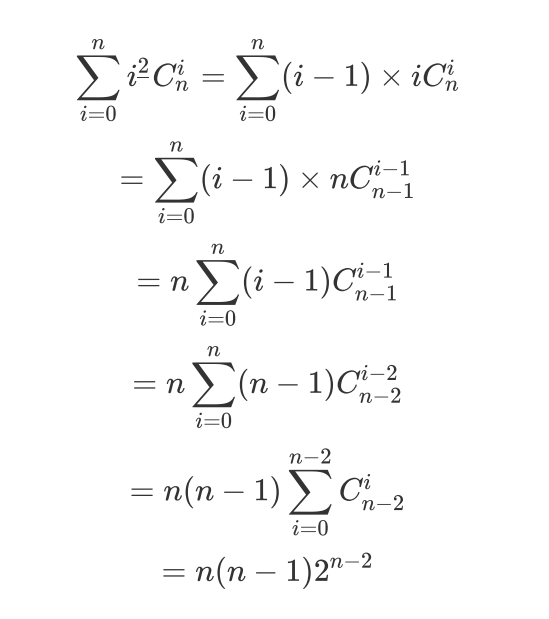
以此类推就可以得出最终答案：

就是

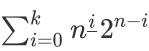
发现用到的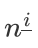只有k个，把它和2ⁱ滚动地处理出来，但需要求n！

所以时间复杂度为O(n)。

拜拜~