MKL库奇异值分解(LAPACKE_dgesvd)

对任意一个\(m\times n\)的实矩阵，总可以按照SVD算法对其进行分解。即：

\[A = U\Sigma V^T
\]

其中\(U、V\)分别为\(m\times m、n\times n\)的方阵，由\(A\)的左奇异向量和右奇异向量组成，且\(U\)与\(V\)均为正交阵。\(\Sigma\)为\(m\times n\)的对角矩阵，对角线上的元素为矩阵\(A\)的奇异值。

在MKL库中求解奇异值和奇异向量的函数为LAPACKE_dgesvd。

1 参数详解

lapack_int LAPACKE_dgesvd(
                            matrix_layout,	// (input)行优先(LAPACK_ROW_MAJOR)或列优先(LAPACK_COL_MAJOR)
                            jobu,		// (input)计算矩阵U的全部或部分并返回。
                                                /*"A":返回U的所有M列到U,
                                                  "S":返回U的前min(m,n)列到U,
                                                  "O":返回U的前min(m,n)列到A矩阵(覆盖),
                                                  "N":不计算矩阵U*/
                            jobvt,		// (input)计算矩阵VT的全部或部分并返回；选项列表与jobu相同；
                            m, 			// (input)A矩阵的行，m>=0
                            n,  		// (input)A矩阵的列，n>=0
                            a, 			// (input/output)A矩阵
                            lda,		// (input)A矩阵的第一维大小
                            s,			// (output)A矩阵的奇异值，并按照从大到小的顺序排列
                            u,			// (output) 矩阵U元素的一维数组
                            ldu, 		// (input) U矩阵的第一维大小
                            vt,			// (output) 矩阵VT元素的一维数组
                            ldvt,		// (input) VT矩阵的第一维大小
                            superb,		// (output)工作空间
                        )

2 定义待处理矩阵

#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"

#define min(a,b) ((a)>(b)?(b):(a))

// 矩阵维度参数
#define M 6
#define N 5
#define LDA N
#define LDU M
#define LDVT N

// 声明需要的参数
MKL_INT m = M, n = N, lda = LDA, ldu = LDU, ldvt = LDVT, info;
double superb[min(M,N)-1];				

double s[N], u[LDU*M], vt[LDVT*N];		//声明奇异值与奇异向量
double a[LDA*M] = {				//定义待分解的A矩阵
    8.79,  9.93,  9.83, 5.45,  3.16,
    6.11,  6.91,  5.04, -0.27,  7.98,
    -9.15, -7.93,  4.86, 4.85,  3.01,
    9.57,  1.64,  8.83, 0.74,  5.80,
    -3.49,  4.02,  9.80, 10.00,  4.27,
    9.84,  0.15, -8.99, -6.02, -5.31
};

3 执行SVD分解

LAPACKE_dgesvd(LAPACK_ROW_MAJOR, 'A', 'A', m, n, a, lda, s, u, ldu, vt, ldvt, superb);

结果如图：

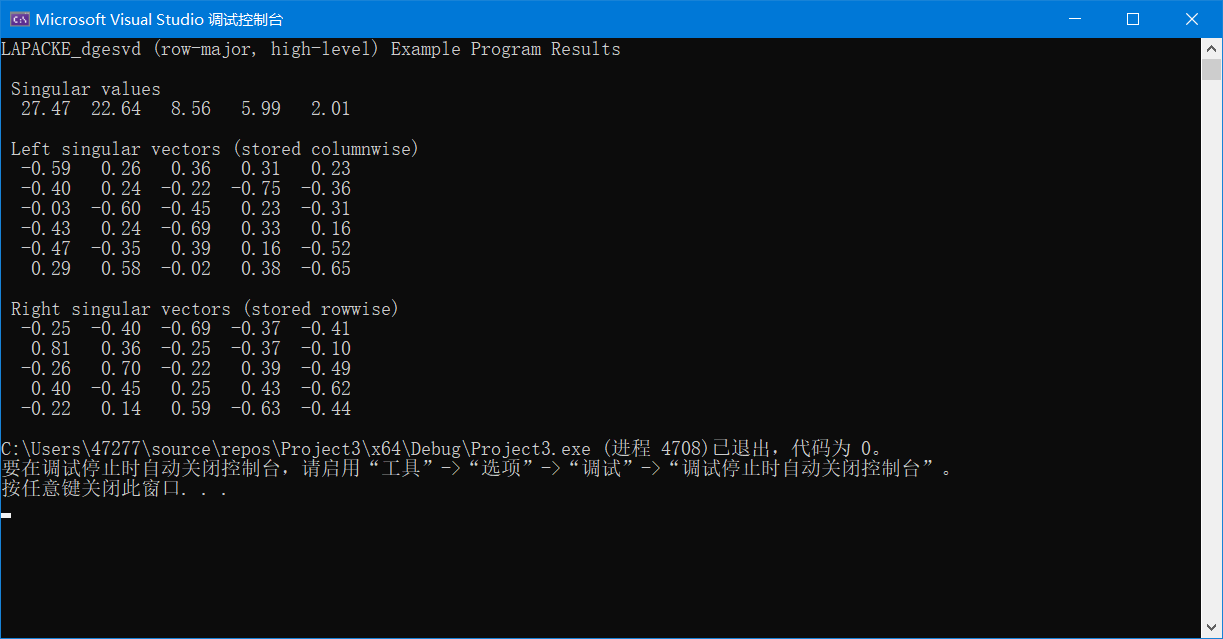
完整代码

#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"

#define min(a,b) ((a)>(b)?(b):(a))

// 展示奇异向量
extern void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda);

#define M 6
#define N 5
#define LDA N
#define LDU M
#define LDVT N

int main() {
	//声明、定义输入
    MKL_INT m = M, n = N, lda = LDA, ldu = LDU, ldvt = LDVT, info;
    double superb[min(M, N) - 1];

    double s[N], u[LDU * M], vt[LDVT * N];
    double a[LDA * M] = {
        8.79,  9.93,  9.83, 5.45,  3.16,
        6.11,  6.91,  5.04, -0.27,  7.98,
       -9.15, -7.93,  4.86, 4.85,  3.01,
        9.57,  1.64,  8.83, 0.74,  5.80,
       -3.49,  4.02,  9.80, 10.00,  4.27,
        9.84,  0.15, -8.99, -6.02, -5.31
    };

    printf("LAPACKE_dgesvd (row-major, high-level) Example Program Results\n");
    //计算SVD
    info = LAPACKE_dgesvd(LAPACK_ROW_MAJOR, 'A', 'A', m, n, a, lda,
        s, u, ldu, vt, ldvt, superb);

    if (info > 0) {
        printf("The algorithm computing SVD failed to converge.\n");
        exit(1);
    }
    //奇异值
    print_matrix("Singular values", 1, n, s, 1);
    //左奇异向量
    print_matrix("Left singular vectors (stored columnwise)", m, n, u, ldu);
    //右奇异向量
    print_matrix("Right singular vectors (stored rowwise)", n, n, vt, ldvt);
    exit(0);
} 

void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda) {
    MKL_INT i, j;
    printf("\n %s\n", desc);
    for (i = 0; i < m; i++) {
        for (j = 0; j < n; j++) printf(" %6.2f", a[i * lda + j]);
        printf("\n");
    }
}

补充：SVD分解求逆

由之前的介绍，对于任意的实数矩阵\(A\)，可以进行SVD分解：

\[A = U\Sigma V^T\\
\]

其中，\(U\)、\(V^T\)为正交矩阵，\(\Sigma\)为对角矩阵。若\(A\)矩阵可逆，易得

\[A^{-1}=(U\Sigma V^T)^{-1}=V\Sigma^{-1}U^T
\]

即当使用LAPACKE_dgesvd，将矩阵\(A\)分解出三部分后，再经过简单的转置、对角阵求逆，最后通过LAPACKE_dgemm完成各矩阵相乘即可得到\(A\)的逆矩阵。