P4012 深海机器人问题

$\color{#0066ff}{题目描述}$

深海资源考察探险队的潜艇将到达深海的海底进行科学考察。

潜艇内有多个深海机器人。潜艇到达深海海底后，深海机器人将离开潜艇向预定目标移动。

深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。

每条预定路径上的生物标本的价值是已知的，而且生物标本只能被采集一次。

本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动，而且多个深海机器人可以在同一时间占据同一位置。

用一个 $P\times Q$ 网格表示深海机器人的可移动位置。西南角的坐标为 $(0,0)$，东北角的坐标为 $(Q,P)$ 。

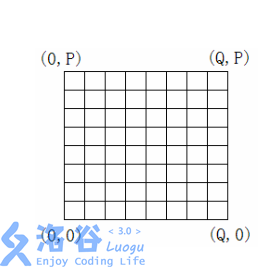
给定每个深海机器人的出发位置和目标位置，以及每条网格边上生物标本的价值。

计算深海机器人的最优移动方案，使深海机器人到达目的地后，采集到的生物标本的总价值最高。

$\color{#0066ff}{输入格式}$

文件的第 $1$ 行为深海机器人的出发位置数 $a$,和目的地数 $b$ 。

第 $2$ 行为 $P$ 和 $Q$ 的值。

接下来的 $P+1$ 行,每行有 $Q$ 个正整数,表示向东移动路径上生物标本的价值,行数据依从南到北方向排列。

再接下来的 $Q+1$ 行,每行有 $P$ 个正整数,表示向北移动路径上生物标本的价值,行数据依从西到东方向排列。

接下来的 $a$ 行,每行有 $3$ 个正整数 $k,x,y$,表示有 $k$ 个深海机器人从 $(x,y)$ 位置坐标出发。

再接下来的 $b$ 行,每行有 $3$ 个正整数 $r,x,y$ ,表示有 $r$ 个深海机器人可选择 $(x,y)$ 位置坐标作为目的地。

$\color{#0066ff}{输出格式}$

输出采集到的生物标本的最高总价值.

$\color{#0066ff}{输入样例}$

$\color{#0066ff}{输出样例}$

$\color{#0066ff}{数据范围与提示}$

$1\leq P,Q\leq 15$

$1\leq a\leq 4$

$1\leq b\leq 6$

$\color{#0066ff}{题解}$

S向所有机器人起点连边

所有机器人终点向T连边

每个点向右向下分别连两条边

一条容量为 1 ，边权为图中边权

另一条容量为 inf，边权为零

这样保证了权值只能获得一次，又保证了这条边可以被多个人走

#include <cstdio>

#include <iostream>

#include <cstring>

#include <algorithm>

#include <queue>

#include <cmath>

#define _ 0

#define LL long long

#define int long long

inline LL in() {

	LL x = 0, f = 1; char ch;

	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);

	while(isdigit(ch)) x = x * 10 + (ch ^ 48), ch = getchar();

	return x * f;

}

const int maxn = 105050;

struct node {

	int to, dis, can;

	node *nxt, *rev;

	node(int to = 0, int dis = 0, int can = 0, node *nxt = NULL):to(to), dis(dis), can(can), nxt(nxt) {}

	void *operator new (size_t) {

		static node *S = NULL, *T = NULL;

		return (S == T) && (T = (S = new node[1024]) + 1024), S++;

	}

};

const int inf = 0x7fffffff;

int n, m, p, q, s, t;

typedef node* nod;

bool vis[maxn];

nod head[maxn], road[maxn];

int dis[maxn], change[maxn], id[55][55];

std::queue<int> V;

inline void add(int from, int to, int can, int dis) {

	nod o = new node(to, dis, can, head[from]);

	head[from] = o;

}

inline void link(int from, int to, int can, int dis) {

	add(from, to, can, dis);

	add(to, from, 0, -dis);

	head[from]->rev = head[to];

	head[to]->rev = head[from];

}

inline bool spfa()

{

	for(int i = s; i <= t; i++) dis[i] = -inf, change[i] = inf;

	V.push(s);

	dis[s] = 0;

	while(!V.empty()) {

		int tp = V.front(); V.pop();

		vis[tp] = false;

		for(nod i = head[tp]; i; i = i->nxt) {

			if(dis[i->to] < dis[tp] + i->dis && i->can > 0) {

				dis[i->to] = dis[tp] + i->dis;

				road[i->to] = i;

				change[i->to] = std::min(change[tp], i->can);

				if(!vis[i->to]) vis[i->to] = true, V.push(i->to);

			}

		}

	}

	return change[t] != inf;

}

inline void mcmf() {

	int cost = 0;

	while(spfa()) {

		cost += dis[t] * change[t];

		for(int o = t; o != s; o = road[o]->rev->to) {

			road[o]->can -= change[t];

			road[o]->rev->can += change[t];

		}

	}

	printf("%lld", cost);

}

signed main() {

	n = in(), m = in(), p = in(), q = in();

	for(int cnt = 0, i = 0; i <= p; i++)

		for(int j = 0; j <= q; j++)

			id[i][j] = ++cnt;

	s = 0, t = id[p][q] + 1;

	for(int i = 0; i <= p; i++)

		for(int j = 0; j < q; j++)

			link(id[i][j], id[i][j+1], 1, in());

	for(int i = 0; i <= q; i++)

		for(int j = 0; j < p; j++)

			link(id[j][i], id[j+1][i], 1, in());

	int k, x, y;

	for(int i = 1; i <= n; i++) {

		k = in(), x = in(), y = in();

		link(s, id[x][y], k, 0);

	}

	for(int i = 1; i <= m; i++) {

		k = in(), x = in(), y = in();

		link(id[x][y], t, k, 0);

	}

	for(int i = 0; i <= p; i++)

        for(int j = 0; j <= q; j++) {

            if(i + 1 <= p) link(id[i][j], id[i+1][j], inf, 0);

            if(j + 1 <= q) link(id[i][j], id[i][j+1], inf, 0);

        }

	mcmf();

	return 0 ;

}