51NOD1174 区间最大数 && RMQ问题（ST算法）

RMQ问题（区间最值问题Range Minimum/Maximum Query）

　　　　ST算法

　　　　RMQ（Range Minimum/Maximum Query），即区间最值查询，是指这样一个问题：对于长度为n的数列a，回答若干询问RMQ（A,i,j）(i, j<=n)，返回数列a中下标在i，j之间的最小/大值。如果只有一次询问，那样只有一遍for就可以搞定，但是如果有许多次询问就无法在很快的时间处理出来。在这里介绍一个在线算法。所谓在线算法，是指用户每输入一个查询便马上处理一个查询。该算法一般用较长的时间做预处理，待信息充足以后便可以用较少的时间回答每个查询。ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

　　　　假设a数组为：

　　　　1， 3， 6， 7， 4， 2， 5

　　　　1.预处理

　　　　设dp[i][j]表示从第i位开始连续2^j个数中的最大值。例如dp[2][1]为第2位数开始连续2个的数的最大值，即6, 4之间的最大值，即mn[2][1] = 4。我们先初始化dp[0...n-1][0]为a数组中的值，之后我们很容易想到递推方程：

　　　　dp[i][j] = max(dp[i][j - 1], dp[i + (1 << j - 1)][j - 1])

20000> 2**14 > 10000
  30000> 2**15 > 40000
  60000> 2**16 > 70000

1 for(int j = ; j < ; j ++)
     for(int i = ; i + ( << j) <= n + ; i ++)
         dp[i][j] = max(dp[i][j - ], dp[i + ( << (j - ))][j - ]);

　　　　2.查询

　　　　假设我们需要查询[lo, hi]之间的最值，我们令k = log2(hi-lo+1)

　　　　由于k是 log2(hi-lo+1)向下取整得到的，所以无法完全覆盖lo到hi

　　　　只要保证lo + k 的长度大于lo到hi的长度的1/2即可使用：RMQ[l, r] = min(dp[l][k], dp[r - (1 << k) + 1][k]);

　　　　

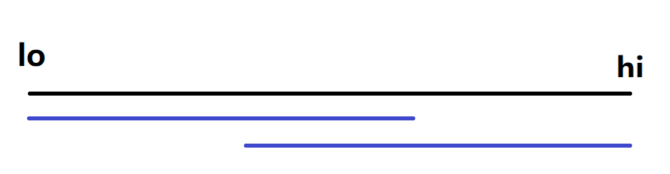
　　　　因为不难看出，对于任意长度len，(int)log2(len) ** 2 > len/2

　　　　所以最终代码如下：

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 using namespace std;
 /*
 20000> 2**14 > 10000
 30000> 2**15 > 40000
 60000> 2**16 > 70000
 */
 int N[];

 int mx[][];

 int main()
 {
     int n,q;
     scanf("%d", &n);
     for(int i=;i<n;i++)
     {
         scanf("%d", &N[i]);
     }
     // -------------------------------

     memset(mx, , sizeof(mx));
     for(int i=;i<n;i++)
     {
         mx[i][] = N[i];
     }

     for(int i=;i<;i++)
     {
         for(int j=;j+(<<i)-<n;j++)
         {
             mx[j][i] = max(mx[j][i-], mx[j+(<<i-)][i-]);
         }
     }

     // -------------------------------
     scanf("%d", &q);
     int lo, hi;
     for(int i=;i<q;i++)
     {
         scanf("%d%d", &lo, &hi);
         int k = (int)log2((double)(hi-lo+));
         int ans = max(mx[lo][k], mx[hi-(<<k)+][k]);
         printf("%d\n", ans);
     }
 }

当然也可以用线段树解决