Python算法应用实战之队列详解

队列是一种先进先出（First-In-First-Out，FIFO）的数据结构。队列被用在很多地方，比如提交操作系统执行的一系列进程、打印任务池等，一些仿真系统用队列来模拟银行或杂货店里排队的顾客。下面就介绍了Python中队列的应用实战，需要的可以参考。

队列（queue）

队列是先进先出（FIFO, First-In-First-Out）的线性表，在具体应用中通常用链表或者数组来实现，队列只允许在后端（称为rear）进行插入操作，在前端（称为front）进行删除操作，队列的操作方式和堆栈类似，唯一的区别在于队列只允许新数据在后端进行添加（摘录维基百科）。

如图所示

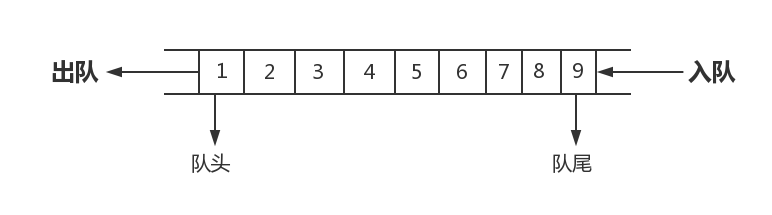
队列的接口

一个队列至少需要如下接口：

接口	描述
add(x)	入队
delete()	出队
clear()	清空队列
isEmpty()	判断队列是否为空
isFull()	判断队列是否未满
length()	队列的当前长度
capability()	队列的容量

然而在Python中，可以使用collections模块下的deque函数，deque函数提供了队列所有的接口，那么先让我门看看队列deque函数提供了那些API把：

collections.deque是双端队列，即左右两边都是可进可出的

方法	描述
append(x)	在队列的右边添加一个元素
appendleft(x)	在队列的左边添加一个元素
clear()	从队列中删除所有元素
copy()	返回一个浅拷贝的副本
count(value)	返回值在队列中出现的次数
extend([x..])	使用可迭代的元素扩展队列的右侧
extendleft([x..])	使用可迭代的元素扩展队列的右侧
index(value, [start, [stop]])	返回值的第一个索引，如果值不存在，则引发ValueError。
insert(index, object)	在索引之前插入对象
maxlen	获取队列的最大长度
pop()	删除并返回最右侧的元素
popleft()	删除并返回最左侧的元素
remove(value)	删除查找到的第一个值
reverse()	队列中的所有元素进行翻转
rotate()	向右旋转队列n步（默认n = 1），如果n为负，向左旋转。

现在我们在Python中测试下这些个API的使用吧。

入队操作

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

>>> from collections import deque # 创建一个队列 >>> q = deque([1]) >>> q deque([1]) # 往队列中添加一个元素 >>> q.append(2) >>> q deque([1, 2]) # 往队列最左边添加一个元素 >>> q.appendleft(3) >>> q deque([3, 1, 2]) # 同时入队多个元素 >>> q.extend([4,5,6]) >>> q deque([3, 1, 2, 4, 5, 6]) # 在最左边同时入队多个元素 >>> q.extendleft([7,8,9]) >>> q deque([9, 8, 7, 3, 1, 2, 4, 5, 6])

出队操作

?

1 2 3 4 5 6 7 8 9 10

# 删除队列中最后一个 >>> q.pop() 6 >>> q deque([9, 8, 7, 3, 1, 2, 4, 5]) # 删除队列中最左边的一个元素 >>> q.popleft() 9 >>> q deque([8, 7, 3, 1, 2, 4, 5])

其他的API

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

# 清空队列 >>> q deque([8, 7, 3, 1, 2, 4, 5]) >>> q.clear() >>> q deque([]) # 判断队列是否为空 >>> not q True # 获取队列最大长度 >>> q = deque([1,2], 10) >>> q.maxlen 10 # 查看某个元素出现的次数 >>> q.extend([1,2,1,1]) >>> q.count(1) 4 # 查看当前队列长度 >>> len(q) 6 # 判断队列是否满了 >>> q.maxlen == len(q) False # 队列元素反转 >>> q = deque([1,2,3,4,5],5) >>> q.reverse() >>> q deque([5, 4, 3, 2, 1], maxlen=5) # 查看元素对应的索引 >>> q.index(1) 4 # 删除匹配到的第一个元素 >>> q deque([5, 4, 3, 2, 1], maxlen=5) >>> q.remove(5) >>> q deque([4, 3, 2, 1], maxlen=5) # 元素位置进行旋转 >>> q deque([4, 3, 2, 1], maxlen=5) >>> q.rotate(2) >>> q deque([2, 1, 4, 3], maxlen=5) >>> q.rotate(1) >>> q deque([3, 2, 1, 4], maxlen=5) # 使用负数 >>> q.rotate(-1) >>> q deque([2, 1, 4, 3], maxlen=5)

实例

二项式系数

题目

编写程序，求二项式系数表中(杨辉三角)第K层系列数

?

1 2 3 4 5

1  1 1  1 2 1 1 3 3 1 ......

思路

1. 把第K行的系数存储在队列中
2. 依次出队K层的系数（每行最后一个1不出队），并推算K+1层系数，添加到队尾，最后在队尾添加一个1，便变成了k+1行。

解决代码

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

#!/use/bin/env python # _*_ coding:utf-8 _*_ from collections import deque def yanghui(k):  """  :param k: 杨辉三角中第几层  :return: 第K层的系数  """  q = deque([1]) # 创建一个队列，默认从1开始  for i in range(k): # 迭代要查找的层数  for _ in range(i): # 循环需要出队多少次   q.append(q.popleft() + q[0]) # 第一个数加上队列中第二个数并赋值到队列末尾  q.append(1) # 每次查找结束后都需要在队列最右边添加个1  return list(q) result = yanghui(3) print(result)

划分无冲突子集

题目

某动物园搬家，要运走N种动物，老虎与狮子放在一起会大家，大象与犀牛放在一个笼子会打架，野猪和野狗放在一个笼子里会打架，现在需要我们设计一个算法，使得装进同一个笼子的动物互相不打架。

思路

1. 把所有动物按次序入队
2. 创建一个笼子(集合)，出队一个动物，如果和笼子内动物无冲冲突则添加到该笼子，有冲突则添加到队尾，等待进入新笼子
3. 由于队列先进先出的特性，如果当前出队动物的index不大于前一个出队动物的index，说明当前队列中所有动物已经尝试过进入且进入不了当前笼子，此时创建信的笼子(集合)

解决代码

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

#!/use/bin/env python # _*_ coding:utf-8 _*_ from collections import deque def division(m, n):  """  :param m: 冲突关系矩阵  :param n: 几种动物  :return: 返回一个栈，栈内包含了所有的笼子  """  res = [] # 创建一个栈  q = deque(range(n)) # 初始化队列，里面放着动物的序号  pre = n # 前一个动物的下标  while q:  cur = q.popleft() # 从队头出队一个动物  if pre >= cur: # 是否需要创建笼子   res.append([]) # 创建一个笼子  # 当前的动物是否与笼子内的动物有冲突  for a in res[-1]: # 迭代栈中最顶层的笼子   if m[cur][a]: # 有冲突   q.append(cur) # 重新放入队列的尾部   break  else: # 当前动物和当前笼子中的所有动物没冲突   res[-1].append(cur) # 当前动物放入最上面的笼子中  pre = cur # 当前变成之前的  return res N = 9 R = { # 冲突对应关系表  (1, 4), (4, 8), (1, 8), (1, 7),  (8, 3), (1, 0), (0, 5), (1, 5),  (3, 4), (5, 6), (5, 2), (6, 2), (6, 4), } M = [[0] * N for _ in range(N)] # 冲洗关系矩阵M，0代表不冲突 for i, j in R:  M[i][j] = M[j][i] = 1 # 1代表冲突 result = division(M, N) print(result)

数字变换

题目

对于一对正整数a,b,对a只能进行加1，减1，乘2操作，问最少对a进行几次操作能得到b？

例如：

1. a=3,b=11: 可以通过322-1，3次操作得到11；
2. a=5,b=8：可以通过(5-1)*2，2次操作得到8；

思路

本题用广度优先搜索，寻找a到b状态迁移最短路径，对于每个状态s，可以转换到撞到s+1,s-1,s*2:

1. 把初始化状态a入队；
2. 出队一个状态s，然后s+1,s-1,s*2入队；
3. 反复循环第二步骤，直到状态s为b；

解决代码

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

#!/use/bin/env python # _*_ coding:utf-8 _*_ from collections import deque def atob(a, b):  """  :param a: 开始的数字  :param b: 最终转换之后的数字  :return: 最小匹配的次数  """  q = deque([(a, 0)]) # a=当前数字，0=操作的次数  checked = {a} # 已经检查过的数据  while True:  s, c = q.popleft()  if s == b:   break  if s < b: # 要计算的数小于计算之后的数字   if s + 1 not in checked: # 如果要计算的数字+1不在已检查过的数据集合中   q.append((s + 1, c + 1)) # 要计算的数+1，转换次数+1   checked.add(s + 1) # 把计算过的数添加到checked集合中   if s * 2 not in checked:   q.append((s * 2, c + 1))   checked.add(s * 2)  if s > 0: # 要计算的数大于0   if s - 1 not in checked:   q.append((s - 1, c + 1))   checked.add(s - 1)  return q.popleft()[-1] result = atob(3, 11) print(result)

总结

以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作能带来一定的帮助，如果有疑问大家可以留言交流。

原文链接：http://www.h5min.cn/article/104517.htm