T7316 yyy的最大公约数(者)

题目背景

全场基本暴力

题目描述

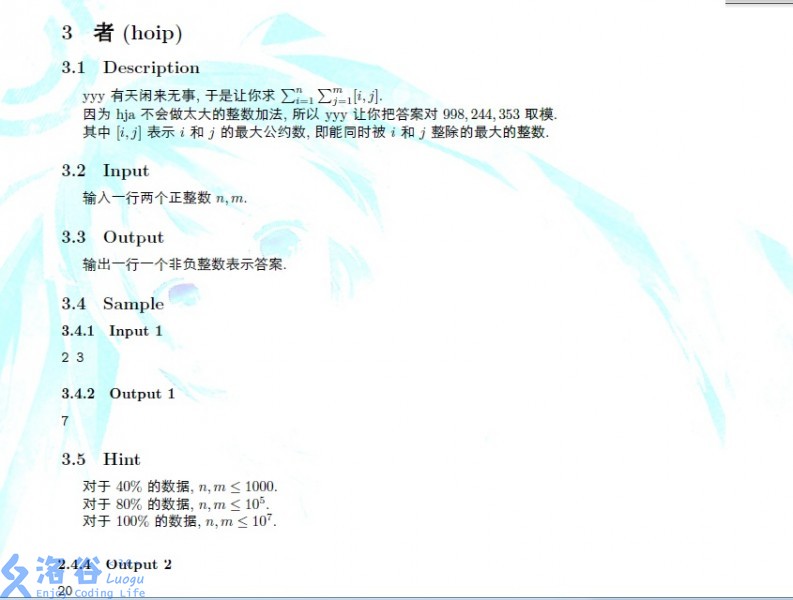
输入输出格式

输入格式：

如图

输出格式：

如图

输入输出样例

输入样例#1：

如图

输出样例#1：

如图

说明

如图

这题用到了容斥原理和线性筛的一些东西，

表示没怎么看懂、。。。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<queue>
 #include<stack>
 #include<cstdlib>
 #define lli long long int
 using namespace std;
 const int mod = ;
 const lli maxn=0x7fffff;

 const lli MAXN=;
 inline void read(lli &n)
 {
     char c='+';lli x=;bool flag=;
     while(c<''||c>''){c=getchar();if(c=='-')flag=;}
     while(c>=''&&c<='')
     x=(x<<)+(x<<)+c-,c=getchar();
     flag==?n=-x:n=x;
 }
 lli n,m;
 lli ans=;
 lli now[MAXN];
 int main()
 {
     read(n);
     read(m);
     if(n>m)
         swap(n,m);

     for(lli i=n;i>=;i--)
     {
         now[i]=1ll*(n/i)*(m/i);
         for(lli j=i+i;j<=n;j+=i)
             now[i]-=now[j];
         ans+=now[i]*i;
     }
     printf("%lld",ans%mod);
     return ;
 }