BZOJ4001 TJOI2015概率论（生成函数+卡特兰数）

　　设f(n)为n个节点的二叉树个数，g(n)为n个节点的二叉树的叶子数量之和。则答案为g(n)/f(n)。

　　显然f(n)为卡特兰数。有递推式f(n)=Σf(i)f(n-i-1) (i=0~n-1)。

　　类似地，左子树节点数为i时右子树有f(n-i-1)种情况，那么可以对左子树的叶子节点数之和计数，显然再乘2就是总数了。有递推式g(n)=2Σg(i)f(n-i-1) (i=0~n-1)。

　　因为递推式是卷积形式，考虑生成函数。设F(x)、G(x)分别为f(n)、g(n)的生成函数（均为无穷级数）。则有F(x)=xF²(x)+1。乘x是为了给他进一位。因为f(0)=f(1)=1，只要补上x^0位上的1就好了。解得F(x)=[1±√(1-4x)]/(2x)。其中√1-4x可以用广义二项式定理计算出来，发现其每一项都是负数，于是我们取F(x)=[1-√(1-4x)]/(2x)。

　　同样的道理，G(x)=2xF(x)G(x)+x。因为g(0)=0，g(1)=1，进一位后需要补上x^1位上的1。解得G(x)=x/√(1-4x)。

　　有了生成函数我们可以暴推原数列了。

　　

　　

　　

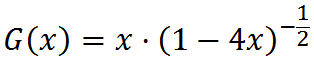
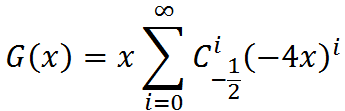
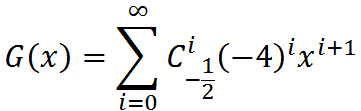
　　即g(n)=C(-1/2,n-1)·(-4)^n-1。这个式子得化的更好看一点。不妨展开组合数。

　　

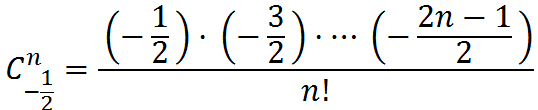
　　则C(-1/2,n)=(2n)!/(2ⁿ·n!)·(-1/2)ⁿ/n!=(-1/4)ⁿ·(2n)!/n!/n!=(-1/4)ⁿ·C(2n,n)。

　　g(n)=(-1/4)^n-1·C(2n-2,n-1)·(-4)^n-1=C(2n-2,n-1)。简直优美到爆炸！

　　我们知道卡特兰数的通项公式是f(n)=C(2n,n)/(n+1)。

　　那么g(n)/f(n)=[(2n-2)!/(n-1)!/(n-1)!]/[(2n)!/n!/n!/(n+1)]=n²(n+1)/(2n)/(2n-1)=n(n+1)/2(2n-1)。

　　于是一句话就做完了。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int read()
{
    int x=,f=;char c=getchar();
    while (c<''||c>'') {if (c=='-') f=-;c=getchar();}
    while (c>=''&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x*f;
}
double n;
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj4001.in","r",stdin);
    freopen("bzoj4001.out","w",stdout);
    const char LL[]="%I64d";
#else
    const char LL[]="%lld";
#endif
    n=read();
    printf("%.9lf",n*(n+)//(*n-));
    return ;
}