unity----------------------四元数的概念

作者：Yang Eninala
链接：https://www.zhihu.com/question/23005815/answer/33971127
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

根据我的理解，大多数人用汉密尔顿四元数就只是做三维空间的旋转变换（我反正没见过其他用法）。那么你不用学群论，甚至不用复习线性代数，看我下面的几张图就可以了。

首先，定义一个你需要做的旋转。旋转轴为向量，旋转角度为（右手法则的旋转）。如下图所示：
此图中,
<img src="https://pic1.zhimg.com/50/c089c595ab174b5c6886bfc4285460f8_hd.jpg" data-rawwidth="1250" data-rawheight="849" class="origin_image zh-lightbox-thumb" width="1250" data-original="https://pic1.zhimg.com/c089c595ab174b5c6886bfc4285460f8_r.jpg">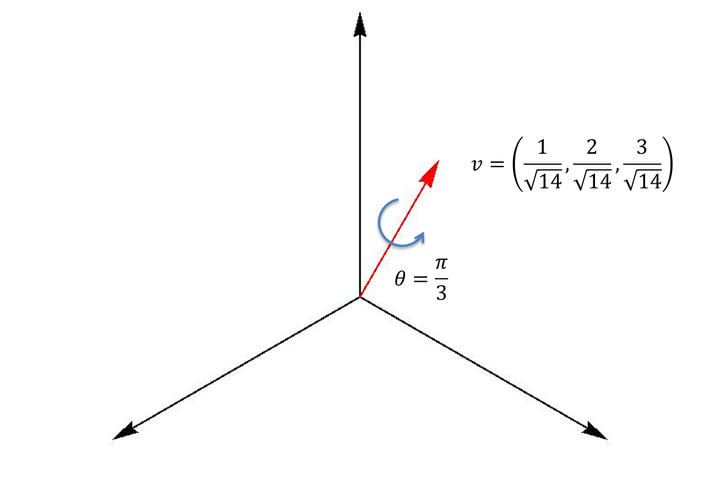

那么与此相对应的四元数（下三行式子都是一个意思，只是不同的表达形式）

这时它的共轭（下三行式子都是一个意思，只是不同的表达形式），

如果你想算一个点在这个旋转下新的坐标,需要进行如下操作，
1.定义纯四元数

2.进行四元数运算

3.产生的一定是纯四元数，也就是说它的第一项为0，有如下形式：

4.中的后三项就是：

这样，就完成了一次四元数旋转运算。

同理，如果你有一个四元数：

那么，它对应一个以向量为轴旋转角度的旋转操作（右手法则的旋转）。

***********************************************************************************************************
如果你想对四元数有着更深入的了解，请往下看。

四元数由汉密尔顿发明，这一发明起源于十九世纪的某一天。在这一天早上，汉密尔顿下楼吃早饭。这时他的儿子问他，“爸爸，我们能够对三元数组（triplet，可以理解为三维向量）做乘法运算么？”汉密尔顿说“不行，我只能加减它们。”

这时来自21世纪的旁白旁先生说，“大家快来看十九世纪的数学家有多二，连内积和外积都不是知道。”

十九世纪的汉密尔顿也许确实不知道内积和外积，但是他知道，他想要的三维向量乘法要比内积和外积运算“高大上”很多。这一乘法运算要满足下列四条性质：
1.运算产生的结果也要是三维向量
2.存在一个元运算，任何三维向量进行元运算的结果就是其本身
3.对于任何一个运算，都存在一个逆运算，这两个运算的积是元运算
4.运算满足结合律

换而言之，汉密尔顿想定义的不是一个简单的映射关系，而是一个群！（后来我们知道四元数所在群为S3，而四元数所代表的三维旋转是SO(3)，前者是后者的两倍覆盖）内积连性质1都不满足，外积不满足性质3。

汉密尔顿先生就这么被自己儿子提出的问题难倒了。经历了无数个日日夜夜，他绞尽脑汁也没想明白这个问题。终于有一天（1843年的一天），汉密尔顿先生终于意识到了，自己所需要的运算在三维空间中是不可能实现的，但在四维空间中是可以的，他是如此的兴奋，以至于把四元数的公式刻在了爱尔兰的一座桥上。

旁白：“WTF，我让你讲三维物体的旋转，你给我扯到四维空间上去。”

（不加说明，以下所说四元数全为单位四元数）
其实，四元数有四个变量，完全可以被看作一个四维向量。单位四元数（norm=1）则存在于四维空间的一个球面上。，四元数乘以四元数其实看作（1）对进行左旋转，或者（2）对进行右旋转。所以从始至终，四元数定义的都是四维旋转，而不是三维旋转！任意的四维旋转都可以唯一的拆分为一个左旋转和一个右旋转，表达出来就是。这里，我们对四元数（四维向量）进行了一个左旋转和一个右旋转。结果当然是一个四元数，符合性质1。这个运算也同时符合性质2，3，4。

好了，说完了四维旋转，我们终于可以说说三维旋转了。说白了，三维旋转就是四维旋转的一个特例，就像二维旋转是三维旋转的一个特例一样。说是特例其实不准确，准确的说是一个子集或者subgroup。为了进行三维旋转运算，汉密尔顿首先在四维空间里划出了一块三维空间。汉密尔顿定义了一种纯四元数（pure quaternion），其表达式为。纯四元数第一项为零，它存在于四维空间的三维超平面上，与三维空间中的三维向量一一对应。然后，就有了我们常见的这种左乘单位四元数，右乘其共轭的表达式。我真心不知道汉密尔顿是怎么想出来的，不过回过头来看，这个运算形式是为了限制其运算结果所在的空间。简单的说，当对一个三维向量进行三维旋转后，我们希望得到的是一个三维向量。（如果你真能得到一个四维向量，就不敢自己在家转圈圈了吧，转着转着，就进入四次元了！）那么这个左乘单位四元数，右乘其共轭的运算保证了结果是一个在三维超平面上中的纯四元数。

把左乘和右乘表达为矩阵形式会让我们看的更清楚一些。依照的定义，的矩阵形式为

很明显，前面的矩阵虽然是一个4x4的四维旋转矩阵，但是它只是在右下角3x3的区域内和一个单位矩阵有所不同。所以说，它是一个限制在三维超平面上的四维旋转。如果表达式右边不是共轭，而是任意四元数，那么我们所作的就是一个很普通的四维旋转。如果只是左乘一个单位四元数，右边什么都不乘，那么我们得到的是四维旋转的一个子集，这个子集并不能保证结果限制在三维超平面上。如果只右乘，不左乘也是一样一样的。

说了这么多，对于坚持到最后的你，上图一幅，以表感谢。
<img src="https://pic2.zhimg.com/50/c1a4657d87e2d863fd00439397783475_hd.jpg" data-rawwidth="1279" data-rawheight="524" class="origin_image zh-lightbox-thumb" width="1279" data-original="https://pic2.zhimg.com/c1a4657d87e2d863fd00439397783475_r.jpg">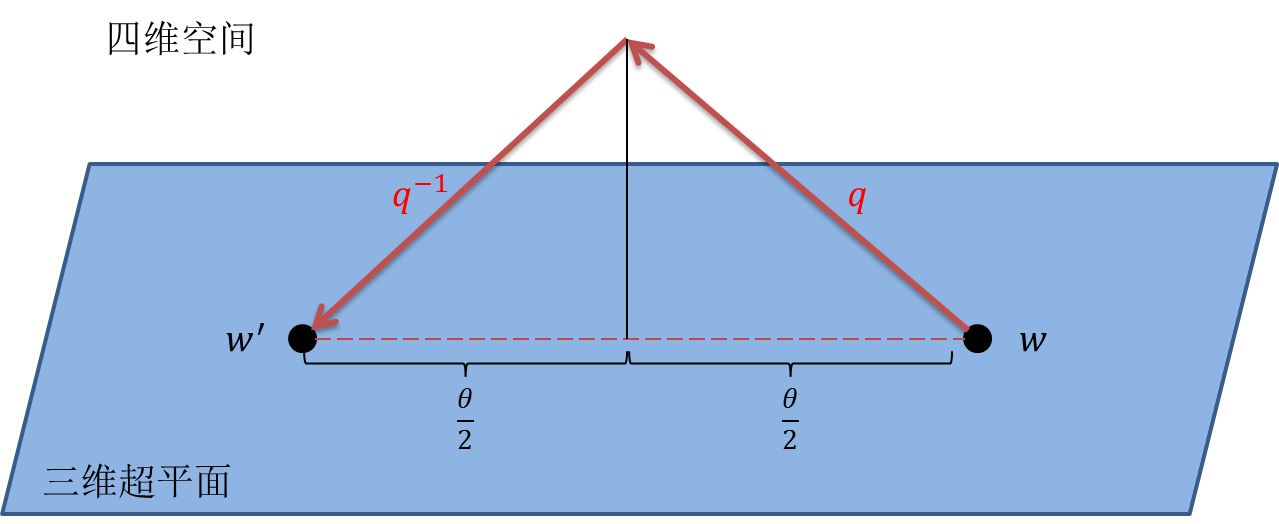
其实这张图解释了一个长久的疑问。为什么四元数里用的是而不是。这是因为做的就是一个的旋转，而也做了一个的旋转。我们进行了两次旋转，而不是一次，这两次旋转的结果是一个旋转角为的旋转。