Doris BloomFilter原理

1、Bloom Filter的核心是一个【m】位的bitset和【k】个hash函数。

初始时bitset中所有位的值都设置为0，假设取【m = 10】，【k = 3】，用蓝色表示某位为0，红色表示为1

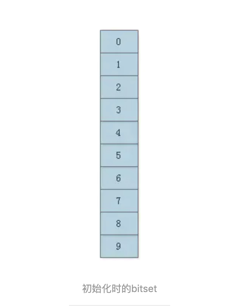
2、插入数据

　　插入元素的过程是三步走：

　　（1）计算k个hash值

　　（2）将k个hash值对m取模得到k个下标

　　（3）将bitset中k个下标对应的位设置为1

　　例：比如向的Bloom Filter插入元素“Alice”。

　　分别用3个hash函数计算“Alice”的hash值，将hash值对10取模，得到在[0, 10)范围内的r1、r2、r3，

　　假设计算结果为：

　　r1 = h1("Alice") % m = 1

　　r2 = h2("Alice") % m = 3

　　r3 = h3("Alice") % m = 5

　　于是将bitset中第1位、第3位和第5位的值置为1

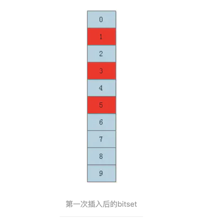
　　再插入元素“Bob”的过程还是一样的，假设：

　　r1 = h1("Bob") % m = 8

　　r2 = h2("Bob") % m = 2

　　r3 = h3("Bob") % m = 3

　　那就将bitset中第2位、第3位、第8位的值置为1（值已经为1的第3位不动）：

　　图形化思考的话就是，Bloom Filter运行过程中不断插入新元素，bitset里的0逐渐被翻转成1。

3、查询数据

　怎么判断元素“Alice”是否在集合里呢？同样还是三步走：

　（1）计算k个hash值

　（2）将k个hash值对m取模得到k个下标

（3）检查bitset中k个下标对应的位是否都为1

　　如果Bloom Filter里有“Alice”，那bitset中相应的k位值显然都为1。问题是即使Bloom Filter里没有“Alice”，

　　还是可能由于之前插入的元素而导致“Alice”对应的k位值都为1，因此会错误地认为集合里已经有“Alice”了，

　　这就是Bloom Filter会出错的地方。

　　【不支持删除】由于bitset里每位都和多个元素有关，将某个为1的位置为0，涉及到这位的元素都会被认为不属于集合，所以Bloom Filter不支持删除操作。

4、复杂度分析

　　空间复杂度方面：Bloom Filter不会动态增长，运行过程中维护的始终只是m位的bitset，所以空间复杂度只有O(m)。

　　时间复杂度方面：Bloom Filter的插入与属于操作主要都是在计算k个hash，所以都是O(k)。

　　参考链接： https://www.jianshu.com/p/8193d7dc8348